Dissecting Stockfish Part 3: In-Depth Look at a chess engine

Navigating a chess tree at scale

Welcome back to our series on the inner workings of the Stockfish chess engine. Our goal is to explain the algorithms and techniques that make Stockfish one of the most powerful chess engines in the world. By understanding these mechanisms, we can gain deeper insights into the intersection of computer science, artificial intelligence, and game theory.

The previous parts of this series explored how Stockfish finds a playable move (part. 1) and evaluates the quality of a position from that move (part. 2). But how to consider what our opponent can play next? And what would be our possible responses?

To handle this situation, Stockfish relies on one final concept: depth.

A tree for all moves

The game begins: pawn to e4. Your opponent responds with e5. Then Nf3, Nc6, and so on. This sequence forms a single branch in the tree of all possible moves.

Stockfish navigates this tree to determine the best move based on all potential outcomes.

The best worst outcome

In game theory, there is a one-fits-all algorithm for turn-based games: the Minimax algorithm. The crux of it is that, because you cannot predict your opponent’s move, you assume they will always choose the best one for themselves.

This is illustrated in the diagram below:

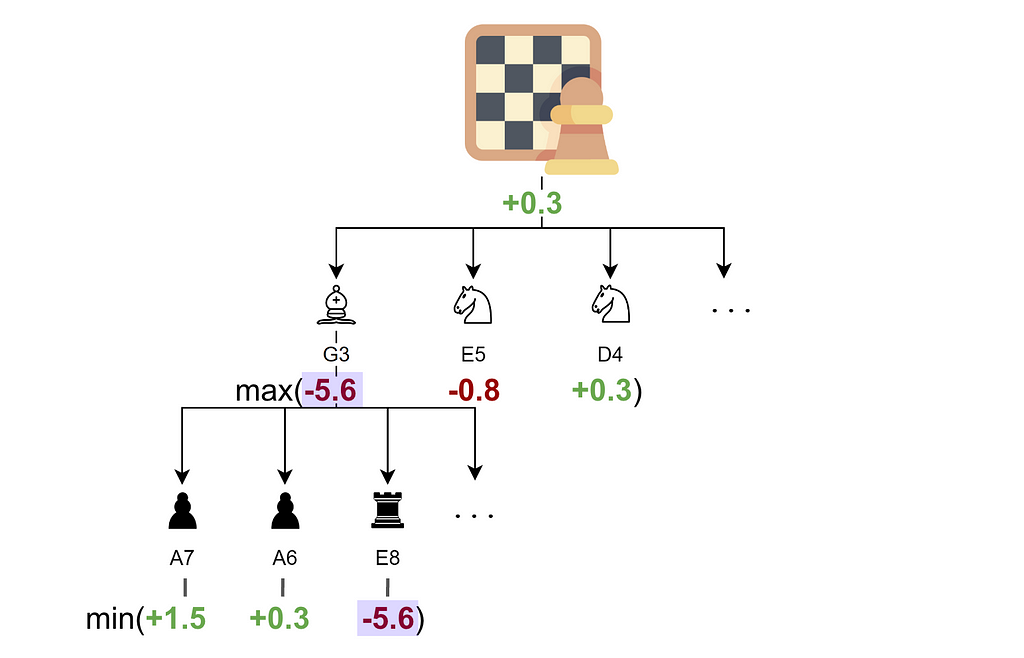
• For the move bishop G3, Stockfish considers all possible responses from the opponent.
• Although some moves, like pawn to A7 or A6, yield a positive score, the move rook to E8 results in a disadvantage of -5.6.
• This worst-case outcome gives the move bishop to G3 a score of -5.6, as it is assumed the opponent (black player) will find and play their best move.
• After calculating all moves and responses, Stockfish selects the best option for itself (white player), which in this case is knight to D4.

Although that example illustrated what happens using a single move with the opponent’s responses, the Minimax algorithm can be extended recursively up to an infinite depth. The limiting factor is computing resources, which leads us to the next section.

Optimization and tradeoff

Even though Stockfish can assess millions of moves per second, it still cannot evaluate an entire chess position in a reasonable time due to the exponential growth of possible moves with each depth level.

For example, Claude Shannon demonstrated that to reach a depth of 10 moves from the starting position, one would need to evaluate 69 billion positions. Using the Minimax algorithm alone, this would take days.

Stockfish leverages several improvements to that Minimax algorithm. One such improvement is Alpha-Beta pruning, which optimizes the traversal of the move tree. This is illustrated below:

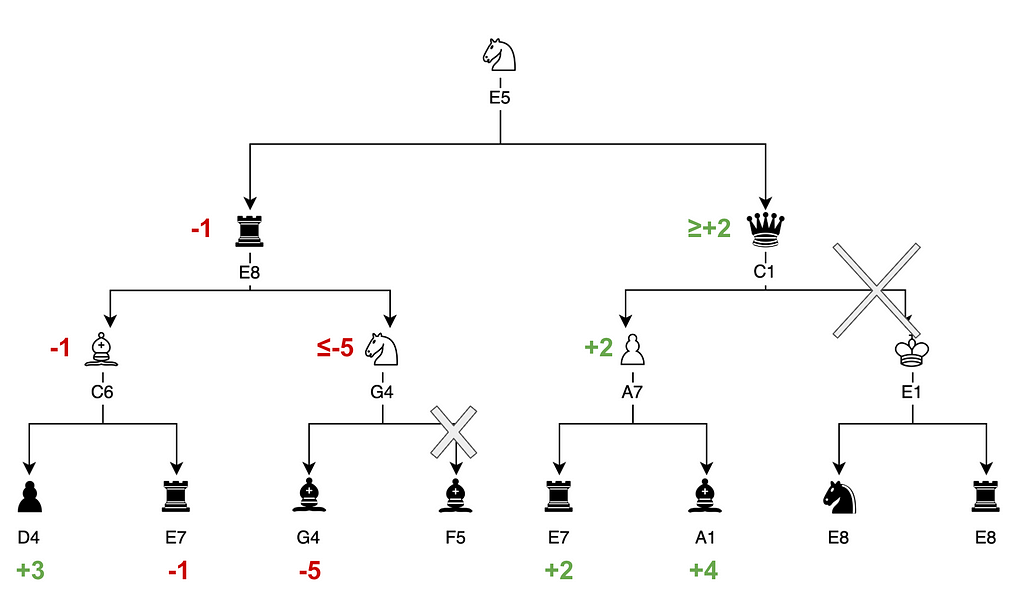
• Stockfish calculated that the sequence rook E8 -> knight G4 -> bishop G4 leads to a disadvantage of -5.
• Another sequence rook E8 -> bishop C6 has already been explored and led to a score of -1, which is better than the branch currently being explored.
• Therefore, knight G4 can be discarded in favor of the better option: bishop C6.

Additional techniques, such as iterative deepening, further enhance the process: when the engine calculates at depth N, it stores the best line of the search, so it can explore these moves first when searching at a depth N+1.

The resulting, big-picture search algorithm for Stockfish is dense (see search.cpp), and yet utilizes another modern computing technique: multithreading.

Distributed search

Modern computers can use multiple threads, allowing Stockfish to scale with distributed computing power.

To do so, Stockfish leverages multiple threads to search for the best move in parallel, with each thread communicating through a concurrent memory storage system.

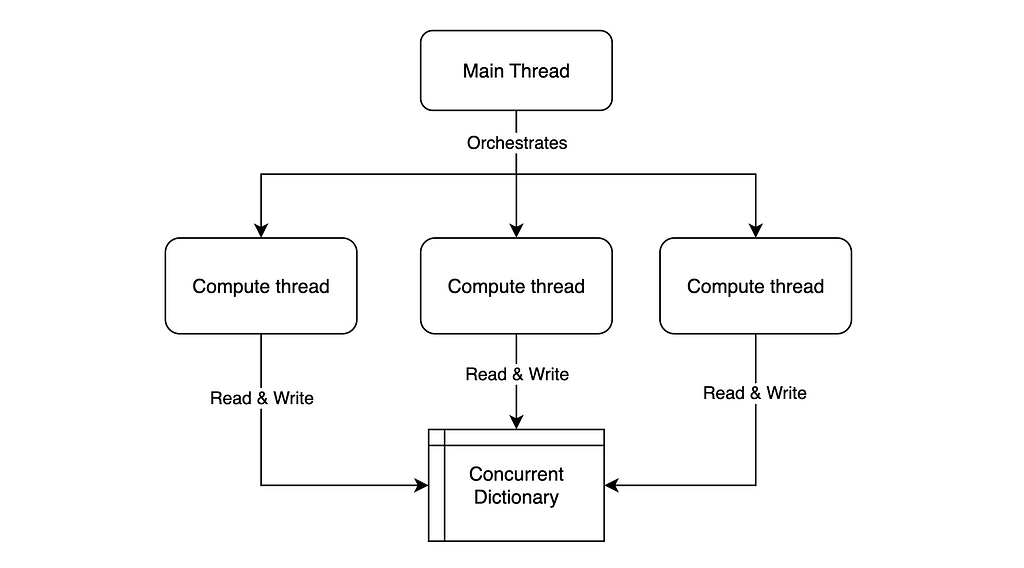
The compute threads are searching the tree in parallel.

• When a thread completes a branch, it writes the result to a shared dictionary.
• When a thread starts a new branch, it checks in that dictionary if any other thread already calculated it.

There is also a main thread that serves as an orchestrator:

• It stores and launches compute threads from a threadpool.
• It seeds initial conditions to each compute thread (e.g. ordering offset for searching the tree, to increase the search entropy and fill the dictionary faster).
• It monitors if a thread finished calculating, in which case it halts all the compute threads and reads the evaluation results from the dictionary.

Interestingly, the few nanoseconds required by memory locks when accessing a “true” concurrent dictionary was too much overhead. Therefore, Stockfish programmers developed their own distributed table (see tt.h).

Conclusion

To summarize:

• Stockfish generates every candidate move for a given depth.
• It evaluates these moves in a tree using various optimizations.
• It increases the evaluation depth, and repeats that process.

Through this series, we’ve uncovered how Stockfish combines classic algorithms with modern computing techniques and neural networks to achieve state-of-the-art performance.

Understanding Stockfish’s inner workings not only demystifies one of the strongest chess engines but also offers broader insights into the challenges and solutions in computing and AI. Due to its inherent nature, Stockfish focuses primarily on efficiency, a theme that is becoming less common in AI as computing power continues to increase. Additionally, Stockfish is an example about how to build a complete, distributed system out of an AI core.

I hope this series has been educational and inspiring. Thank you for reading!

For further reading, you can consult the Chess Programming Wiki and join the Computer Chess Club forum for discussions on chess programming.

https://antoinechampion.com

Dissecting Stockfish Part 3: In-Depth Look at a chess engine was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.