Exploring Medusa and Multi-Token Prediction

This blog post will go into detail on the “MEDUSA: Simple LLM Inference Acceleration Framework with Multiple Decoding Heads” paper

The internet is an incredibly competitive place. Studies show that customers leave webpages if it takes longer than 5 seconds for the webpage to load [2][3]. This poses a challenge for most Large Language Models (LLMs), as they are without a doubt one of the slowest programs out there. While custom hardware can dramatically speed up your LLM, running on this hardware is currently expensive. If we can find ways to make the most of standard hardware, we will be able to dramatically increase the customer experience for LLMs.

The authors of the “MEDUSA: Simple LLM Inference Acceleration Framework with Multiple Decoding Heads” paper have an architectural change that when run on existing hardware achieves a 2x–3x speed up.

Let’s dive in!

Speculative Decoding

Speculative Decoding was introduced as a way to speed up inferencing for an LLM. You see, LLMs are autoregressive, meaning we take the output token that we just predicted and use it to help predict the next token we want. Typically we are predicting one-token at a time (or one-token per forward pass of the neural network). However, because the attention pattern for the next token is very similar to the attention pattern from the previous one, we are repeating most of the same calculations and not gaining much new information.

Speculative decoding means that rather than doing one forward pass for one token, instead after one forward pass we try to find as many tokens as we can. In general there are three steps for this:

(1) Generate the candidates

(2) Process the candidates

(3) Accept certain candidates

Medusa is a type of speculative decoding, and so its steps map directly onto these. Medusa appends decoding heads to the final layer of the model as its implementation of (1). Tree attention is how it processes the candidates for (2). Finally, Medusa uses either rejection sampling or a typical acceptance scheme to accomplish (3). Let’s go through each of these in detail.

Decoding Heads & Medusa

A decoding head takes the internal representation of the hidden state produced by a forward pass of the model and then creates the probabilities that correspond to different tokens in the vocabulary. In essence, it is converting the things the model has learned into probabilities that will determine what the next token is.

Medusa adjusts the architecture of a typical Transformer by appending multiple decoding heads to the last hidden layer of the model. By doing so, it can predict more than just one token given a forward pass. Each additional head that we add predicts one token further. So if you have 3 Medusa heads, you are predicting the first token from the forward pass, and then 3 more tokens after that with the Medusa heads. In the paper, the authors recommend using 5, as they saw this gave the best balance between speed-up and quality.

To accomplish this, the authors of the paper proposed the below decoder head for Medusa:

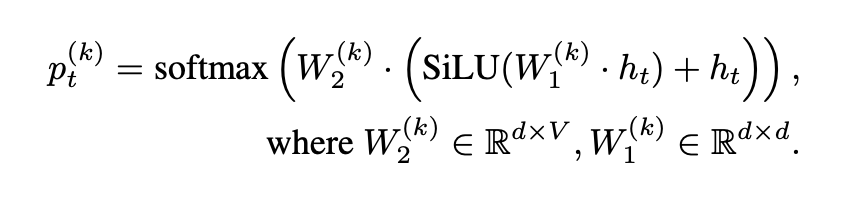
This equation gives us the probability of token t from the k-th head. We start off by using the weights we’ve found through training the Medusa head, W1, and multiplying them by our internal state for token t. We use the SiLU activation function to pass through only selective information(SiLU = x * sigmoid(x)). We add to this the internal state a second time as part of a skip connection, which allows the model to be more performant by not losing information during the linear activation of the SiLU. We then multiply the sum by the second set of weights we’ve trained for the head, W2, and run that product through a softmax to get our probability.

Tree Attention

The first Medusa heads give the model probabilities they should consider based off the forward pass, but the subsequent Medusa heads need to figure out what token they should pick based off what the prior Medusa heads chose.

Naturally, the more options the earlier Medusa heads put forward (hyperparameter sk), the more options future heads need to consider. For example, when we consider just the top two candidates from head 1 (s1=2) and the top three from head 2 (s2=3), we wind up with 6 different situations we need to compute.

Due to this expansion, we would like to generate and verify these candidates as concurrently as possible.

The above matrix shows how we can run all of these calculations within the same batch via tree attention. Unlike typical causal self-attention, only the tokens from the same continuation are considered relevant for the attention pattern. As the matrix illustrates with this limited space, we can fit our candidates all into one batch and run attention on them concurrently.

The challenge here is that each prediction needs to consider only the candidate tokens that would be directly behind it. In other words, if we choose “It” from head 1, and we are evaluating which token should come next, we do not want to have the attention pattern for “I” being used for the tokens.

The authors avoid this kind of interference by using a mask to avoid passing data about irrelevant tokens into the attention calculation. By using this mask, they can be memory efficient while they calculate the attention pattern & then use that information in the decoding head to generate the subsequent token candidates.

While the above matrix shows us considering every prediction the same, if we have a probability for each prediction, we can treat these differently based on how likely they are to be the best choice. The below tree visualizes just that.

In the above, there are 4 Medusa heads each giving multiple candidates. However, not every prediction gets calculated. We add nodes onto our tree based off the probability of them being right. Here, the tree is heavily weighted towards the left, showing that the higher the probability of the prediction, the more possibilities it is shown. In short, what we are doing here is only loading in predictions to the tree attention that we feel have a reasonable likelihood of being the best choice.

Using probability to determine which calculations to continue with is a mindset we’ll see again with the candidate acceptance criteria we’re about to discuss.

Typical Acceptance Scheme vs Rejection Sampling

Now we reach the final stage, determining which predictions to use (if any). As we said from the start, models are auto-regressive, so if we predict the next 5 tokens from the forward-pass, we can simply put in those next 5 into the model for the next go around and enjoy the inference speed increase. However, we only want to do so if the predictions we are getting are high quality. How do we determine this?

One method is Rejection Sampling where we have a separate model that can determine if the next token is good enough (this was used by Meta in their Ghost Attention fine-tuning, learn more here). Naturally, this method is fully dependent on the quality of your other model. If it is good enough, then this works great! Note, however, that to maintain low latency, you’ll want this other model to run quite fast, a difficult thing to balance with high quality.

As a consequence of that difficulty, the authors came up with the typical acceptance scheme to make the determination. As all of the predictions are probabilities, we can use them to set a threshold above which we accept a token. The below equation shows how we do so:

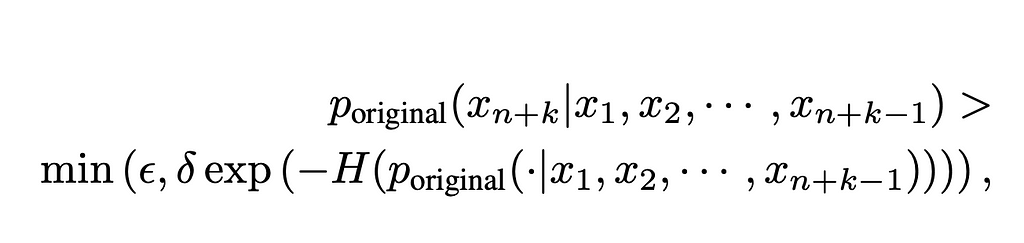
The key here is that we are going to use the probabilities generated by the original model on these tokens to determine if the predictions are valid. We have tokens X1 through Xn as the context for our model to determine the probability for token Xn+k. p represents the probability distribution of our original model, while ϵ and δ are thresholds set to determine when a probability is high enough to merit being included in the model response. The big picture here is that high probability tokens will flow through, but so will tokens that have lower probabilities yet come from a probability distribution where most of the probabilities are low.

Moreover, this function leads to important behavior when we adjust temperature. In general, users increase temperature on an LLM to give more creative responses. Thus, when the temperature is set at zero, typical acceptance ensures that only the first token predicted from the forward pass comes through, giving the most consistent results. However, as the temperature increases, the probability distribution of the LLM changes, leaving us with more predictions that could reach the threshold to be accepted. This leads to both faster results but often times more creative ones as well.

Self-Distillation

The authors propose that to create Medusa models we don’t train from scratch but rather take high-quality foundation models (we’ll call this the backbone part of the model) and add the Medusa heads on top of these. Once we’ve fine-tuned them to understand the new heads, the speed will increase without major performance loss.

Nevertheless fine-tuning requires quality data. The authors were kind enough to explain how they created the data corpus needed to train Medusa.

First, they used the ShareGPT dataset to find high-quality interactions that people expect to have with their LLM. They took all the prompts from the dataset and then ran these through the backbone model to get the ground-truth to fine-tune on.

While this worked well for fine-tuning the Medusa heads (Medusa-1 which we’ll go into below more), this did not work well when fine-tuning the entire new model.

This degradation implied that the ground-truth was not enough information to retrain the model with and still retain high performance. Instead, they rewrote the loss function so that it used the probability distributions as the ground-truth. This required reformulating their loss function like the below.

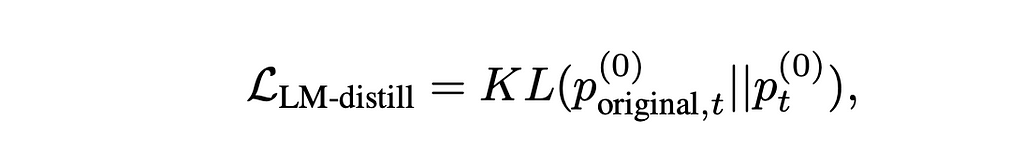
To briefly explain, we’re using Kullback–Leibler divergence (KL) to measure the difference between the original probability distribution for a token and the new probability distribution (to learn more about KL, there is a wonderful post by Aparna Dhinakaran on the topic).

This formulation, however, requires that we maintain the probabilities of both the original and the new model — which is both storage and memory intensive. To reduce our consumption, the authors recommend using LoRA to fine-tune, as this naturally maintains the original weights and the additional weights (to learn more about LoRA check out my blog post on the topic).

Training Medusa

Now that we have the data, we can begin to fine-tune!

As we’ve seen, Medusa requires adding additional parameters to the model to allow this to work, which we’ll have to train. To reduce the amount of computations (and thus training cost) required, the authors introduced two forms of fine-tuning for Medusa: Medusa-1 and Medusa-2.

Medusa-1

Medusa-1 involves freezing all of the weights in the model except for the ones in the Medusa heads. By only running the gradient through the Medusa heads we don’t worry about reducing the performance of the original model (it remains the same), and we can increase the performance of the Medusa heads. The loss function below shows how they match the correct ground-truth token to the correct Medusa head.

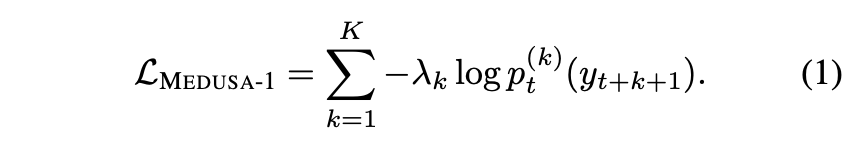
Medusa-1’s focus on only the additional Medusa weights means that it is more cost-effective than Medusa-2 (which we’ll dive into in a moment). For people who are price-sensitive with training, the authors recommend using a quantized backbone model to further reduce memory requirements along with using the Quantized Low Rank Adaptation (QLoRA) fine-tuning methodology to further reduce costs.

Medusa-2

While Medusa-1 is more cost-effective, the best performance still comes when we update all of the weights in the model to account for the new Medusa heads we’ve added. Interestingly, this was not as straight-forward as simply doing LoRA with the gradient passing to all of the weights (rather than just the Medusa weights).

Instead, the authors first ran Medusa-1 to get the Medusa weights to a reasonable performance. Then they chose separate learning rates for the Medusa weights and the backbone model weights. Logically, this was done because the backbone weights were likely close to where they already needed to be, while the Medusa weights should change more. Finally, they added the loss function for the backbone model (denoted Llm) with the Medusa-1 loss function scaled by a value λ0. This lambda is done to balance the loss so that we do not compute an overly large loss value on account of the Medusa heads alone.

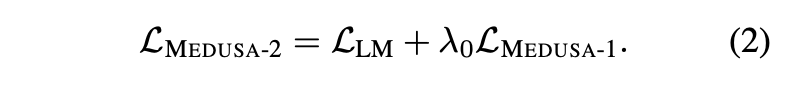
Closing

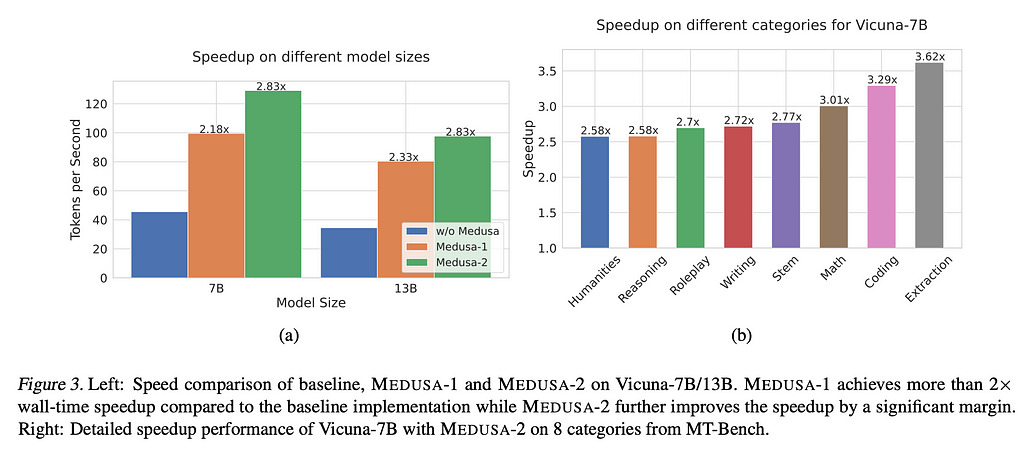
Using Medusa leads to fairly radical improvements in speed. From the graph above, we see that the authors attained between a two to three times speedup for Vicuna — a popular open-source LLM.

Speed is critically important, both on the internet and also on device. As we’ve seen more companies push to create local LLMs, methods like Medusa seem critical to getting great speed on limited hardware. It would be very interesting to see how much a small model like Phi-3 would speed up (at publishing time Phi-3 ran at 12 tokens per second on the A16 Bionic iPhone chip — see my blog post for more information). For developers, this may open the door to running many different kinds of open-source models locally — even if they weren’t initially designed for fast inference like Phi-3.

Moreover, it would be interesting to run experiments on how much of the forward pass’ attention pattern Medusa heads need to increase performance. Right now they have very little context but still perform well. With more context, perhaps the number of Medusa heads could be increased to achieve even better speed up.

It’s an exciting time to be building.

[1] Cai, T., et al, “MEDUSA: Simple LLM Inference Acceleration Framework with Multiple Decoding Heads” (2024), arXiv

[2] Clabaugh, J., “How long do you wait for a webpage to load?” (2022), wtop

[3] Das, S., “How fast should a website load in 2023?” (2023), BrowserStack

Exploring Medusa and Multi-Token Prediction was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.