Unveiling the Inner Workings of LLMs: A Singular Value Perspective

A singular values analysis on Llama3–8B projection matrices

Have you ever thought of how well-trained an LLM is? Given the huge number of parameters, are those parameters capturing the information or knowledge from the training data to the maximum capacity? If not, can we remove the not-useful parameters from the LLM to make it more efficient?

In this article, we’ll try to answer those questions by doing a deep analysis of the Llama-3–8B model from the Singular Values point of view. Without further ado, make ourselves comfortable, and be ready to apply SVD on analyzing Llama-3–8B matrices quality!

SVD Revisited

In Singular Value Decomposition (SVD), a matrix A is decomposed into three other matrices:

A=U Σ V_t

where:

• A is the original matrix.
• U is a matrix whose columns are the left singular vectors of A.
• Σ is a diagonal matrix containing the singular values of A. These values are always non-negative and usually ordered from largest to smallest.
• V_t is the transpose of V, where the columns of V are the right singular vectors of A.

In simpler terms, SVD breaks down the complex transformation of a matrix into simpler, understandable steps involving rotations and scaling. The singular values in Σ tell us the scaling factors and the singular vectors in U and V_t tell us the directions of these scalings before and after applying the matrix.

We can think of the singular values as a way to measure how much a matrix stretches or shrinks in different directions in space. Each singular value corresponds to a pair of singular vectors: one right singular vector (direction in the input space) and one left singular vector (direction in the output space).

So, singular values are the scaling factor that represents the “magnitude”, while the U and V_t matrices represent the “directions” in the transformed space and original space, respectively.

If singular values of matrices exhibit a rapid decay (the largest singular values are significantly larger than the smaller ones), then it means the effective rank of the matrix (the number of significant singular values) is much smaller than the actual dimension of the matrix. This implies that the matrix can be approximated well by a lower-rank matrix.

The large singular values capture most of the important information and variability in the data, while the smaller singular values contribute less.

In the context of LLMs, the weight matrices (e.g., those in the attention mechanism or feedforward layers) transform input data (such as word embeddings) into output representations. The dominant singular values correspond to the directions in the input space that are most amplified by the transformation, indicating the directions along which the model is most sensitive or expressive. The smaller singular values correspond to directions that are less important or less influential in the transformation.

The distribution of singular values can impact the model’s ability to generalize and its robustness. A slow decay (many large singular values) can lead to overfitting, while a fast decay (few large singular values) can indicate underfitting or loss of information.

Llama-3 Architecture Revisited

The following is the config.json file of the meta-llama/Meta-Llama-3–8B-Instructmodel. It is worth noting that this LLM utilizes Grouped Query Attention with num_key_value_heads of 8, which means the group size is 32/8=4.

{
  "architectures": [
    "LlamaForCausalLM"
  ],
  "attention_bias": false,
  "attention_dropout": 0.0,
  "bos_token_id": 128000,
  "eos_token_id": 128009,
  "hidden_act": "silu",
  "hidden_size": 4096,
  "initializer_range": 0.02,
  "intermediate_size": 14336,
  "max_position_embeddings": 8192,
  "model_type": "llama",
  "num_attention_heads": 32,
  "num_hidden_layers": 32,
  "num_key_value_heads": 8,
  "pretraining_tp": 1,
  "rms_norm_eps": 1e-05,
  "rope_scaling": null,
  "rope_theta": 500000.0,
  "tie_word_embeddings": false,
  "torch_dtype": "bfloat16",
  "transformers_version": "4.40.0.dev0",
  "use_cache": true,
  "vocab_size": 128256
}

Singular Values Analysis on (Q, K, V, O) Matrices

Now, let’s jump into the real deal of this article. Analyzing (Q, K, V, O) matrices of Llama-3–8B-Instruct model via their singular values!

The Code

Let’s first import all necessary packages needed in this analysis.

import transformers
import torch
import numpy as np
from transformers import AutoConfig, LlamaModel
from safetensors import safe_open
import os
import matplotlib.pyplot as plt

Then, let’s download the model and save it into our local /tmpdirectory.

MODEL_ID = "meta-llama/Meta-Llama-3-8B-Instruct"
!huggingface-cli download {MODEL_ID} --quiet --local-dir /tmp/{MODEL_ID}

If you’re GPU-rich, the following code might not be relevant for you. However, if you’re GPU-poor like me, the following code will be really useful to load only specific layers of the LLama-3–8B model.

def load_specific_layers_safetensors(model, model_name, layer_to_load):
    state_dict = {}
    files = [f for f in os.listdir(model_name) if f.endswith('.safetensors')]
    for file in files:
        filepath = os.path.join(model_name, file)
        with safe_open(filepath, framework="pt") as f:
            for key in f.keys():
                if f"layers.{layer_to_load}." in key:
                    new_key = key.replace(f"model.layers.{layer_to_load}.", 'layers.0.')
                    state_dict[new_key] = f.get_tensor(key)

    missing_keys, unexpected_keys = model.load_state_dict(state_dict, strict=False)
    if missing_keys:
        print(f"Missing keys: {missing_keys}")
    if unexpected_keys:
        print(f"Unexpected keys: {unexpected_keys}")

The reason we do this is because the free tier of Google Colab GPU is not enough to load LLama-3–8B even with fp16 precision. Furthermore, this analysis requires us to work on fp32 precision due to how the np.linalg.svd is built. Next, we can define the main function to get singular values for a given matrix_type , layer_number , and head_number.

def get_singular_values(model_path, matrix_type, layer_number, head_number):
    """
    Computes the singular values of the specified matrix in the Llama-3 model.

    Parameters:
    model_path (str): Path to the model
    matrix_type (str): Type of matrix ('q', 'k', 'v', 'o')
    layer_number (int): Layer number (0 to 31)
    head_number (int): Head number (0 to 31)

    Returns:
    np.array: Array of singular values
    """
    assert matrix_type in ['q', 'k', 'v', 'o'], "Invalid matrix type"
    assert 0 <= layer_number < 32, "Invalid layer number"
    assert 0 <= head_number < 32, "Invalid head number"

    # Load the model only for that specific layer since we have limited RAM even after using fp16
    config = AutoConfig.from_pretrained(model_path)
    config.num_hidden_layers = 1
    model = LlamaModel(config)
    load_specific_layers_safetensors(model, model_path, layer_number)

    # Access the specified layer
    # Always index 0 since we have loaded for the specific layer
    layer = model.layers[0]

    # Determine the size of each head
    num_heads = layer.self_attn.num_heads
    head_dim = layer.self_attn.head_dim

    # Access the specified matrix
    weight_matrix = getattr(layer.self_attn, f"{matrix_type}_proj").weight.detach().numpy()
    if matrix_type in ['q','o']:
        start = head_number * head_dim
        end = (head_number + 1) * head_dim
    else:  # 'k', 'v' matrices
        # Adjust the head_number based on num_key_value_heads
        # This is done since llama3-8b use Grouped Query Attention
        num_key_value_groups = num_heads // config.num_key_value_heads
        head_number_kv = head_number // num_key_value_groups
        start = head_number_kv * head_dim
        end = (head_number_kv + 1) * head_dim

    # Extract the weights for the specified head
    if matrix_type in ['q', 'k', 'v']:
        weight_matrix = weight_matrix[start:end, :]
    else:  # 'o' matrix
        weight_matrix = weight_matrix[:, start:end]

    # Compute singular values
    singular_values = np.linalg.svd(weight_matrix, compute_uv=False)

    del model, config

    return list(singular_values)

It is worth noting that we can extract the weights for the specified head on the K, Q, and V matrices by doing row-wise slicing because of how it is implemented by HuggingFace.

As for the O matrix, we can do column-wise slicing to extract the weights for the specified head on the O weight thanks to linear algebra! Details can be seen in the following figure.

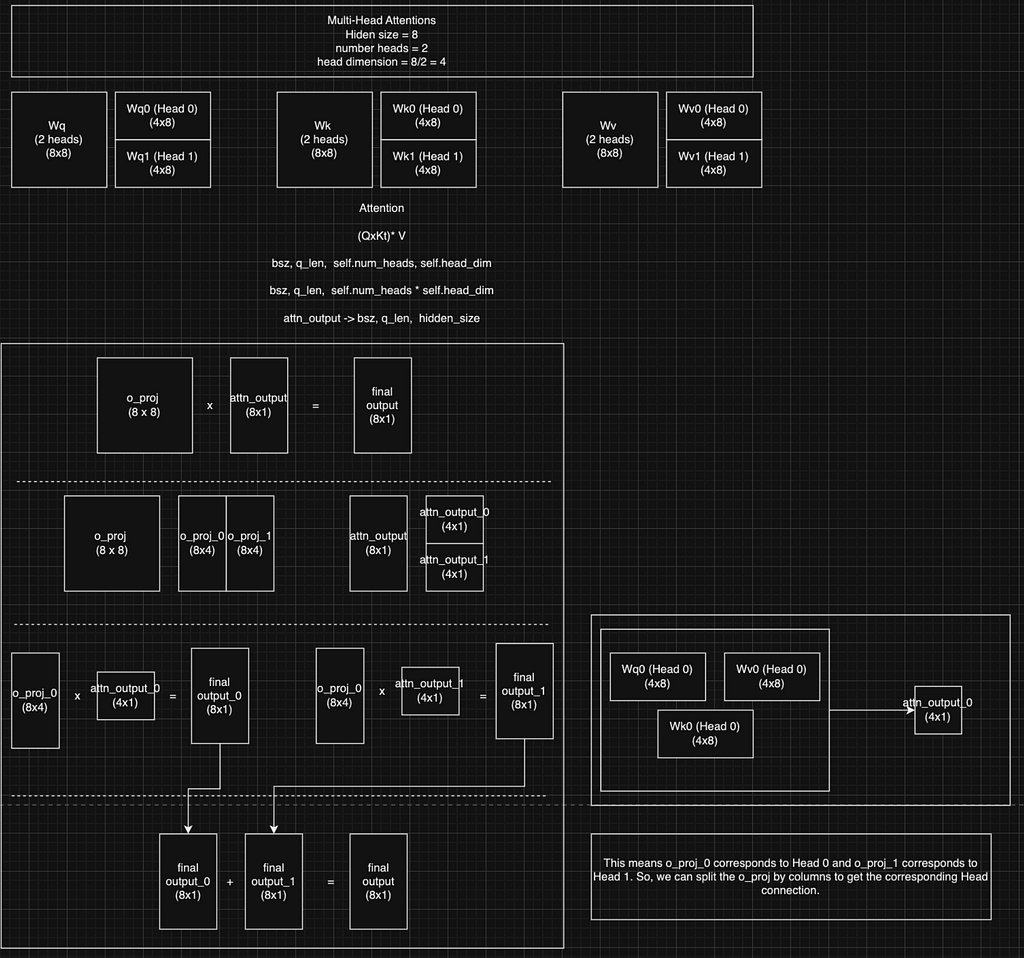
The Results

To do the analysis, we need to run the get_singular_values() function across different heads, layers, and matrix types. And in order to be able to compare across all those different combinations, we also need to define several helper metrics for our analysis:

• Top-10 Ratio : the ratio between the sum of top-10 singular values and sum of all singular values
• First/Last Ratio : the ratio between the highest and lowest singular values.
• Least-10 Ratio : the ratio between the sum of least-10 singular values and sum of all singular values

(Layer 0, Head 0) Analysis

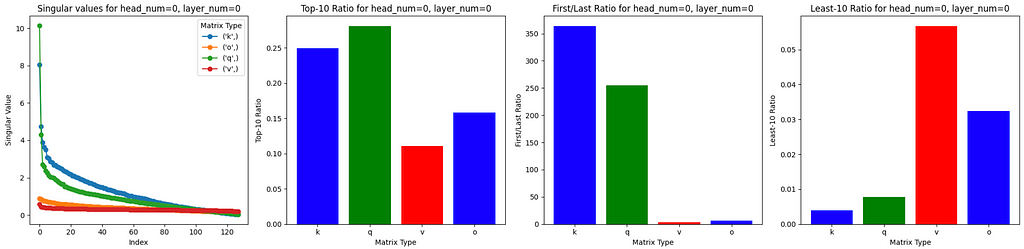
• The Q(query) matrix has the largest initial singular value (~ 10), followed by the K(key) matrix (~ 8). These 2 matrices have significantly higher initial singular values than the initial singular values for V(value) and O(output) matrices.
• Not only initial singular value, if we check the Top-10 Ratioand First/Last Ratio for the Q and K matrices, these two have much higher values compared to V and O matrices. This suggests that the information captured by Q and K matrices mostly focuses on a few dimensions, while for v and o matrices, information is captured in a more dispersed manner across components.
• If we look at the Least-10 Ratiometric, we can also see that for Q and K matrices, the singular values are near zero and relatively much lower compared to the Vand O matrices’. This is one piece of evidence that indicates Q and K matrices have low-rank structure, which indicates that those dimensions contribute little to the overall performance of the model. These weights can potentially be pruned structurally without significantly impacting the model’s accuracy.

(Layer 0, Multiple heads) Analysis

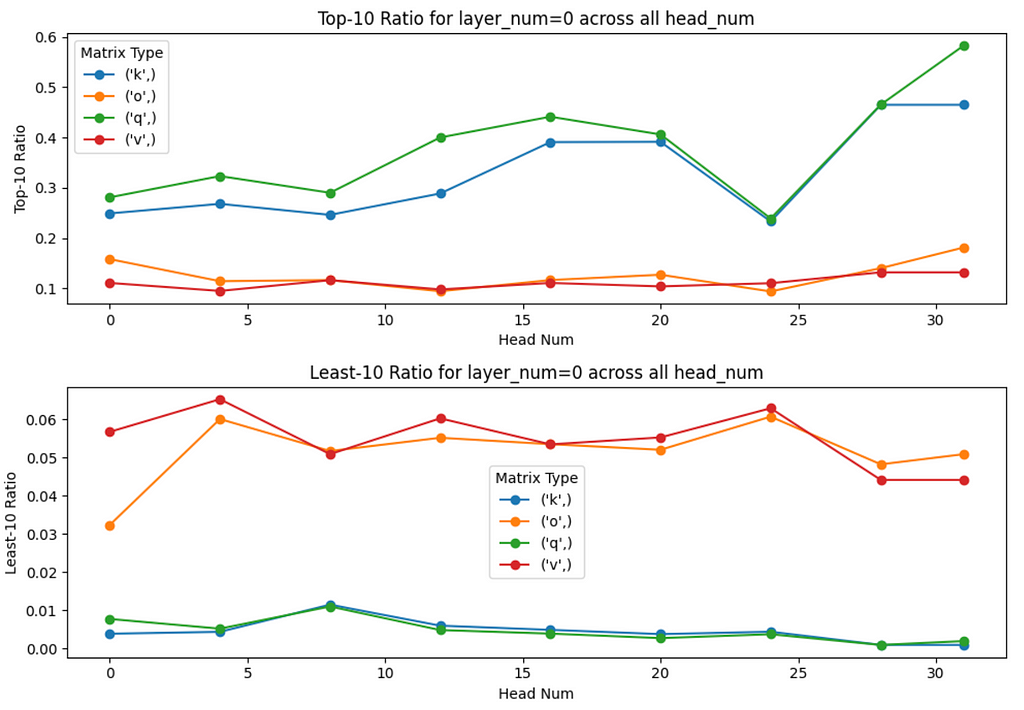
• As the head_number increases, the Top-10 Ratio for Q and K matrices tends to increase at a much higher rate compared to V and O matrices. This insight also applies to the Least-10 Ratio of Q and K matrices where they are becoming nearer to 0 as the head_number increases, while not for the V and O matrices.
• This indicates that Q and K matrices for heads with higher head_number even have a lower rank structure compared to heads with lower head_number. In other words, as the head_number increases, the Q and K matrices tend to store information in even lesser dimensions.

Cross-Layers Analysis

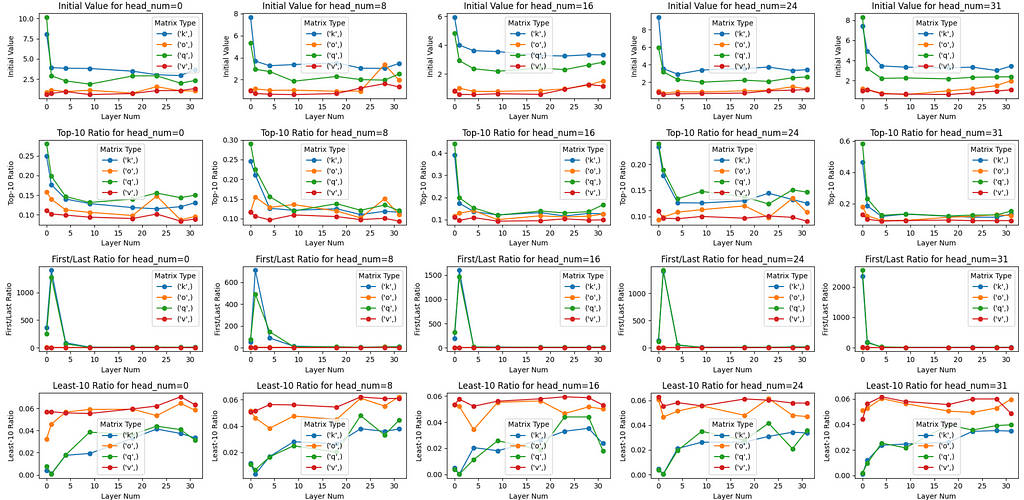
• As we go to deeper layers, we found that initial values of the Q and K matrices are decreasing, but still relatively higher compared to the V and O matrices.
• As we go to deeper layers, there is a downtrend pattern found for the Top-10 Ratio and First/Last Ratio of the Q and K matrices for a particular head. There is also a slight uptrend pattern for the Least-10 Ratio metric. This suggests that Q and K matrices in deeper layers are more well-trained compared to lower layers.

However, there’s an anomaly found in Layer 1 where the First/Last Ratiofor Q and K matrices are incredibly high, not following the downtrend pattern as we go to deeper layers.

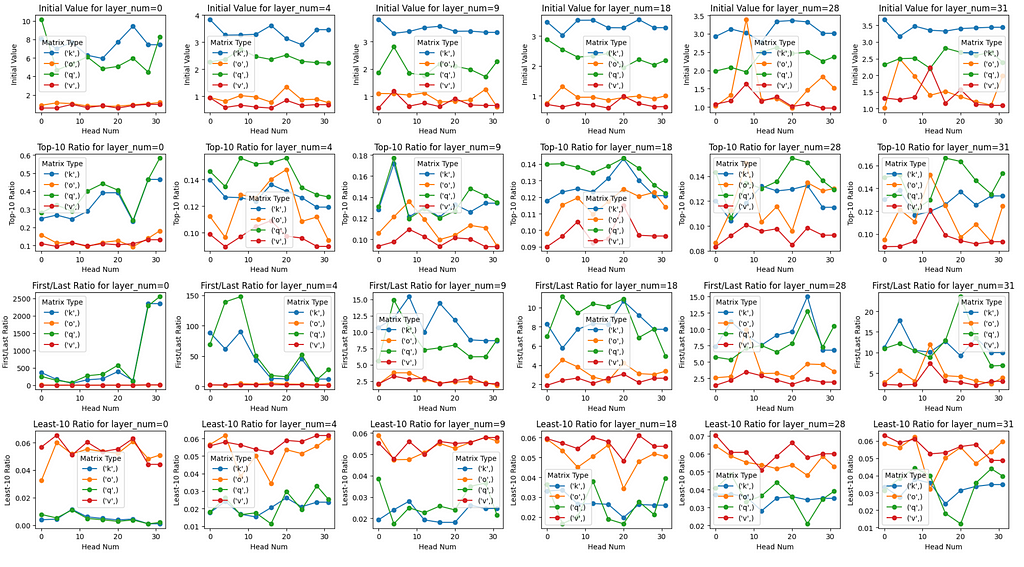
• The pattern across heads within the same layer that we found in the “Layer 0, Multiple Heads” section is not clear when we go to deeper layers.

Summing Up

• The K and Q matrices have relatively lower ranks compared to the V and O matrices. If we want to perform pruning or dimensionality reduction methods, we can focus more on the K and Q matrices.
• The deeper the layers, the more well-trained all (K, Q, V, O) matrices are. If we want to perform pruning or dimensionality reduction methods, we can focus more on lower layers.
• Besides pruning, it’s also interesting to experiment by doing full finetuning only on several initial layers, or we can even do this with LoRA.

Final Words

Congratulations on keeping up to this point! Hopefully, you have learned something new from this article. It is indeed interesting to apply old good concepts from linear algebra to understand how well-trained an LLM is.

If you love this type of content, please kindly follow my Medium account to get notifications for other future posts.

About the Author

Louis Owen is a data scientist/AI research engineer from Indonesia who is always hungry for new knowledge. Throughout his career journey, he has worked in various fields of industry, including NGOs, e-commerce, conversational AI, OTA, Smart City, and FinTech. Outside of work, he loves to spend his time helping data science enthusiasts to become data scientists, either through his articles or through mentoring sessions.

Currently, Louis is an NLP Research Engineer at Yellow.ai, the world’s leading CX automation platform. Check out Louis’ website to learn more about him! Lastly, if you have any queries or any topics to be discussed, please reach out to Louis via LinkedIn.

Unveiling the Inner Workings of LLMs: A Singular Value Perspective was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.