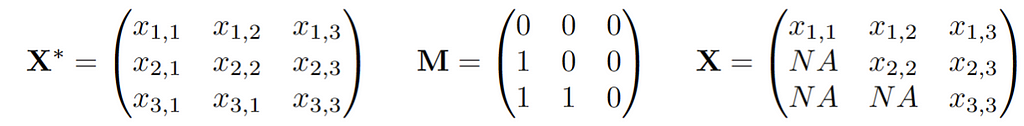What Is a Good Imputation for Missing Values?

My current take on what imputation should be

This article is a first article summarizing and discussing my most recent paper on arXiv. We study general-purpose imputation of tabular datasets. That is, the imputation should be done in a way that works for many different tasks in a second step (sometimes referred to as “broad imputation”).

In this article, I will write 3 lessons that I learned working on this problem over the last years. I am very excited about this paper in particular, but also cautious, as the problem of missing values has many aspects and it can be difficult to not miss something. So I invite you to judge for yourself if my lessons make sense to you.

If you do not want to get into great discussions about missing values, I will summarize my recommendations at the end of the article.

Disclaimer: The goal of this article is to use imputation to recreate the original data distribution. While I feel this is what most researchers and practitioners actually want, this is a difficult goal that might not be necessary in all applications. For instance, when performing (conditional mean) prediction, there are several recent papers showing that even simple imputation methods are sufficient for large sample sizes.

Preliminaries

Before continuing we need to discuss how I think about missing values in this article.

We assume there is an underlying distribution P* from which observations X* are drawn. In addition, there is a vector of 0/1s of the same dimension as X* that is drawn, let’s call this vector M. The actual observed data vector X is then X* masked by M. Thus, we observe n independently and identically distributed (i.i.d.) copies of the joint vector (X,M). If we write this up in a data matrix, this might look like this:

As usual small values x, m means “observed”, while large values refer to random quantities. The missingness mechanisms everyone talks about are then assumptions about the relationship or joint distribution of (X*,M):

Missing Completely at Random (MCAR): The probability of a value being missing is a coin flip, independent of any variable in the dataset. Here missing values are but a nuisance. You could ignore them and just focus on the fully observed part of your dataset and there would be no bias. In math for all m and x:

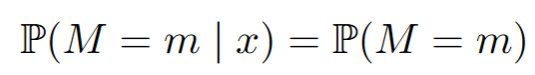
Missing at Random (MAR): The probability of missingness can now depend on the observed variables in your dataset. A typical example would be two variables, say income and age, whereby age is always observed, but income might be missing for certain values of age. This is the example we study below. This may sound reasonable, but here it can get complicated. In math, for all m and x:

Missing Not at Random (MNAR): Everything is possible here, and we cannot say anything about anything in general.

The key is that for imputation, we need to learn the conditional distribution of missing values given observed values in one pattern m’ to impute in another pattern m.

A well-known method of achieving this is the Multiple Imputation by Chained Equations (MICE) method: Initially fill the values with a simple imputation, such as mean imputation. Then for each iteration t, for each variable j regress the observed X_j on all other variables (which are imputed). Then plug in the values of these variables into the learned imputer for all X_j that are not observed. This is explained in detail in this article, with an amazing illustration that will make things immediately clear. In R this is conveniently implemented in the mice R package. As I will outline below, I am a huge fan of this method, based on the performance I have seen. In fact, the ability to recreate the underlying distribution of certain instances of MICE, such as mice-cart, is uncanny. In this article, we focus on a very simple example with only one variable missing, and so we can code by hand what MICE would usually do iteratively, to better illustrate what is happening.

A first mini-lesson is that MICE is a host of methods; whatever method you choose to regress X_j on the other variables gives you a different imputation method. As such, there are countless variants in the mice R package, such as mice-cart, mice-rf, mice-pmm, mice-norm.nob, mice-norm.predict and so on. These methods will perform widely differently as we will see below. Despite this, at least some papers (in top conferences such as NeurIPS) confidently proclaim that they compare their methods to “MICE”, without any detail on what exactly they are using.

The Example

We will look at a very simple but illustrative example: Consider a data set with two jointly normal variables, X_1, X_2. We assume both variables have variance of 1 and a positive correlation of 0.5. To give some context, we can imagine X_1 to be (the logarithm of) income and X_2 to be age. (This is just for illustration, obviously no one is between -3 and 3 years old). Moreover, assume a missing mechanism for the income X_1, whereby X_1 tends to be missing whenever age is “high”. That is we set:

So X_1 (income) is missing with probability 0.8 whenever X_2 (age) is “large” (i.e., larger zero). As we assume X_2 is always observed, this is a textbook MAR example with two patterns, one where all variables are fully observed (m1) and a second (m2), wherein X_1 is missing. Despite the simplicity of this example, if we assume that higher age is related to higher income, there is a clear shift in the distribution of income and age when moving from one pattern to the other. In pattern m2, where income is missing, values of both the observed age and the (unobserved) income tend to be higher. Let’s look at this in code:

library(MASS)
library(mice)



set.seed(10)
n<-3000

Xstar <- mvrnorm(n=n, mu=c(0,0), Sigma=matrix( c(1,0.7,0.7,1), nrow=2, byrow=T   ))

colnames(Xstar) <- paste0("X",1:2)



## Introduce missing mechanisms
M<-matrix(0, ncol=ncol(Xstar), nrow=nrow(Xstar))
M[Xstar[,2] > 0, 1]<- sample(c(0,1), size=sum(Xstar[,2] > 0), replace=T, prob = c(1-0.8,0.8) )


## This gives rise to the observed dataset by masking X^* with M:
X<-Xstar
X[M==1] <- NA


## Plot the distribution shift
par(mfrow=c(2,1))
plot(Xstar[!is.na(X[,1]),1:2], xlab="", main="", ylab="", cex=0.8, col="darkblue", xlim=c(-4,4), ylim=c(-3,3))
plot(Xstar[is.na(X[,1]),1:2], xlab="", main="", ylab="", cex=0.8, col="darkblue", xlim=c(-4,4), ylim=c(-3,3))

Lesson 1: Imputation is a distributional prediction problem

In my view, the goal of (general purpose) imputation should be to replicate the underlying data distribution as well as possible. To illustrate this, consider again the first example with p=0, such that only X_1 has missing values. We will now try to impute this example, using the famous MICE approach. Since only X_1 is missing, we can implement this by hand. We start with the mean imputation, which simply calculates the mean of X_1 in the pattern where it is observed, and plugs this mean in the place of NA. We also use the regression imputation which is a bit more sophisticated: We regress X_1 onto X_2 in the pattern where X_1 is observed and then for each missing observation of X_1 we plug in the prediction of the regression. Thus here we impute the conditional mean of X_1 given X_2. Finally, for the Gaussian imputation, we start with the same regression of X_1 onto X_2, but then impute each missing value of X_1 by drawing from a Gaussian distribution. In other words, instead of imputing the conditional expectation (i.e. just the center of the conditional distribution), we draw from this distribution. This leads to a random imputation, which may be a bit counterintuitive at first, but will actually lead to the best result:

## (0) Mean Imputation: This would correspond to "mean" in the mice R package ##


# 1. Estimate the mean
meanX<-mean(X[!is.na(X[,1]),1])

## 2. Impute
meanimp<-X
meanimp[is.na(X[,1]),1] <-meanX

## (1) Regression Imputation: This would correspond to "norm.predict" in the mice R package ##

# 1. Estimate Regression
lmodelX1X2<-lm(X1~X2, data=as.data.frame(X[!is.na(X[,1]),])   )

## 2. Impute
impnormpredict<-X
impnormpredict[is.na(X[,1]),1] <-predict(lmodelX1X2, newdata= as.data.frame(X[is.na(X[,1]),])  )


## (2) Gaussian Imputation: This would correspond to "norm.nob" in the mice R package ##

# 1. Estimate Regression
#lmodelX1X2<-lm(X1~X2, X=as.data.frame(X[!is.na(X[,1]),])   )
# (same as before)

## 2. Impute
impnorm<-X
meanx<-predict(lmodelX1X2, newdata= as.data.frame(X[is.na(X[,1]),])  )
var <- var(lmodelX1X2$residuals)
impnorm[is.na(X[,1]),1] <-rnorm(n=length(meanx), mean = meanx, sd=sqrt(var) )



## Plot the different imputations

par(mfrow=c(2,2))


plot(meanimp[!is.na(X[,1]),c("X2","X1")], main=paste("Mean Imputation"), cex=0.8, col="darkblue", cex.main=1.5)
points(meanimp[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )

plot(impnormpredict[!is.na(X[,1]),c("X2","X1")], main=paste("Regression Imputation"), cex=0.8, col="darkblue", cex.main=1.5)
points(impnormpredict[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )

plot(impnorm[!is.na(X[,1]),c("X2","X1")], main=paste("Gaussian Imputation"), col="darkblue", cex.main=1.5)
points(impnorm[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )

#plot(Xstar[,c("X2","X1")], main="Truth", col="darkblue", cex.main=1.5)
plot(Xstar[!is.na(X[,1]),c("X2","X1")], main="Truth", col="darkblue", cex.main=1.5)
points(Xstar[is.na(X[,1]),c("X2","X1")], col="darkgreen", cex=0.8 )

Studying this plot immediately reveals that the mean and regression imputations might not be ideal, as they completely fail at recreating the original data distribution. In contrast, the Gaussian imputation looks pretty good, in fact, I’d argue it would be hard to differentiate it from the truth. This might just seem like a technical notion, but this has consequences. Imagine you were given any of those imputed data sets and now you would like to find the regression coefficient when regressing X_2 onto X_1 (the opposite of what we did for imputation). The truth in this case is given by beta=cov(X_1,X_2)/var(X_1)=0.7.

## Regressing X_2 onto X_1

## mean imputation estimate
lm(X2~X1, data=data.frame(meanimp))$coefficients["X1"]
## beta= 0.61

## regression imputation estimate
round(lm(X2~X1, data=data.frame(impnormpredict))$coefficients["X1"],2)
## beta= 0.90

## Gaussian imputation estimate
round(lm(X2~X1, data=data.frame(impnorm))$coefficients["X1"],2)
## beta= 0.71

## Truth imputation estimate
round(lm(X2~X1, data=data.frame(Xstar))$coefficients["X1"],2)
## beta= 0.71

The Gaussian imputation is pretty close to 0.7 (0.71), and importantly, it is very close to the estimate using the full (unobserved) data! On the other hand, the mean imputation underestimates beta, while the regression imputation overestimates beta. The latter is natural, as the conditional mean imputation artificially inflates the relationship between variables. This effect is particularly important, as this will result in effects that are overestimated in science and (data science) practice!!

The regression imputation might seem overly simplistic. However, the key is that very commonly used imputation methods in machine learning and other fields work exactly like this. For instance, knn imputation and random forest imputation (i.e., missForest). Especially the latter has been praised and recommended in several benchmarking papers and appears very widely used. However, missForest fits a Random Forest on the observed data and then simply imputes by the conditional mean. So, using it in this example the result would look very similar to the regression imputation, thus resulting in an artificial strengthening of relations between variable and biased estimates!

A lot of commonly used imputation methods, such as mean imputation, knn imputation, and missForest fail at replicating the distribution. What they estimate and approximate is the (conditional) mean, and so the imputation will look like that of the regression imputation (or even worse for the mean imputation). Instead, we should try to impute by drawing from estimated (conditional) distributions.

Lesson 2: Imputation should be evaluated as a distributional prediction problem

There is a dual problem connected to the discussion of the first lesson. How should imputation methods be evaluated?

Imagine we developed a new imputation method and now want to benchmark this against methods that exist already such as missForest, MICE, or GAIN. In this setting, we artificially induce the missing values and so we have the actual data set just as above. We now want to compare this true dataset to our imputations. For the sake of the example, let us assume the regression imputation above is our new method, and we would like to compare it to mean and Gaussian imputation.

Even in the most prestigious conferences, this is done by calculating the root mean squared error (RMSE):

This is implemented here:

## Function to calculate the RMSE:
# impX is the imputed data set
# Xstar is the fully observed data set

RMSEcalc<-function(impX, Xstar){
  
  round(mean(apply(Xstar - impX,1,function(x) norm(as.matrix(x), type="F"  ) )),2)
  
}

This discussion is related to the discussion on how to correctly score predictions. In this article, I discussed that (R)MSE is the right score to evaluate (conditional) mean predictions. It turns out the exact same logic applies here; using RMSE like this to evaluate our imputation, will favor methods that impute the conditional mean, such as the regression imputation, knn imputation, and missForest.

Instead, imputation should be evaluated as a distributional prediction problem. I suggest using the energy distance between the distribution of the fully observed data and the imputation “distribution”. Details can be found in the paper, but in R it is easily coded using the nice “energy” R package:

library(energy)

## Function to calculate the energy distance:
# impX is the imputed data set
# Xstar is the fully observed data set

## Calculating the energy distance using the eqdist.e function of the energy package
energycalc <- function(impX, Xstar){
  
  # Note: eqdist.e calculates the energy statistics for a test, which is actually
  # = n^2/(2n)*energydistance(impX,Xstar), but we we are only interested in relative values
  round(eqdist.e( rbind(Xstar,impX), c(nrow(Xstar), nrow(impX))  ),2)
  
}

We now apply the two scores to our imaginary research project and try to figure out whether our regression imputation is better than the other two:

par(mfrow=c(2,2))


## Same plots as before, but now with RMSE and energy distance 
## added

plot(meanimp[!is.na(X[,1]),c("X2","X1")], main=paste("Mean Imputation", "nRMSE", RMSEcalc(meanimp, Xstar), "nEnergy", energycalc(meanimp, Xstar)), cex=0.8, col="darkblue", cex.main=1.5)
points(meanimp[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )

plot(impnormpredict[!is.na(X[,1]),c("X2","X1")], main=paste("Regression Imputation","nRMSE", RMSEcalc(impnormpredict, Xstar), "nEnergy", energycalc(impnormpredict, Xstar)), cex=0.8, col="darkblue", cex.main=1.5)
points(impnormpredict[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )

plot(impnorm[!is.na(X[,1]),c("X2","X1")], main=paste("Gaussian Imputation","nRMSE", RMSEcalc(impnorm, Xstar), "nEnergy", energycalc(impnorm, Xstar)), col="darkblue", cex.main=1.5)
points(impnorm[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )


plot(Xstar[!is.na(X[,1]),c("X2","X1")], main="Truth", col="darkblue", cex.main=1.5)
points(Xstar[is.na(X[,1]),c("X2","X1")], col="darkgreen", cex=0.8 )

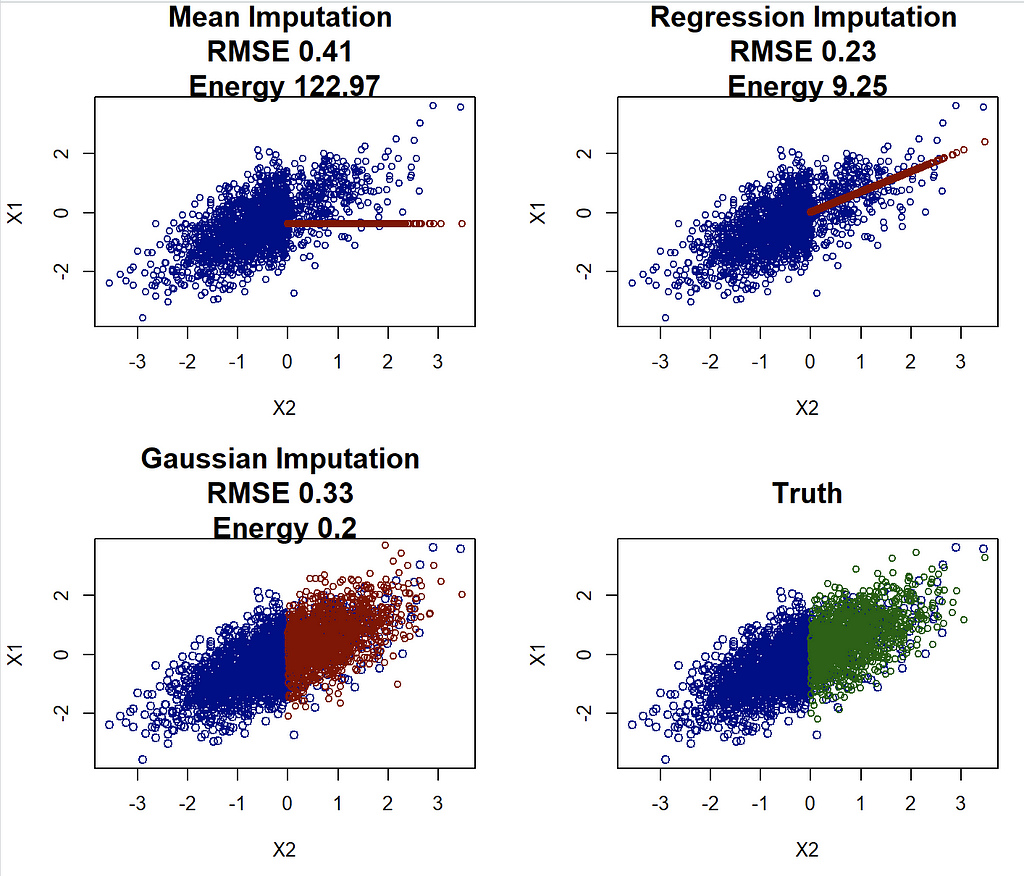
If we look at RMSE, then our regression imputation appears great! It beats both mean and Gaussian imputation. However this clashes with the analysis from above, and choosing the regression imputation can and likely will lead to highly biased results. On the other hand, the (scaled) energy distance correctly identifies that the Gaussian imputation is the best method, agreeing with both visual intuition and better parameter estimates.

When evaluating imputation methods (when the true data are available) measures such as RMSE and MAE should be avoided. Instead, the problem should be treated and evaluated as a distributional prediction problem, and distributional metrics such as the energy distance should be used. The overuse of RMSE as an evaluation tool has some serious implications for research in this area.

Again this is not surprising, identifying the best mean prediction is what RMSE does. What is surprising, is how consistently it is used in research to evaluate imputation methods. In my view, this throws into question at least some recommendations of recent papers, about what imputation methods to use. Moreover, as new imputation methods get developed they are compared to other methods in terms of RMSE and are thus likely not replicating the distribution correctly. One thus has to question the usefulness of at least some of the myriad of imputation methods developed in recent years.

The question of evaluation gets much harder, when the underlying observations are not available. In the paper we develope a score that allows to rank imputation methods, even in this case! (a refinement of the idea presented in this article). The details are reserved for another medium post, but we can try it for this example. The “Iscore.R” function can be found on Github or at the end of this article.

library(mice)
source("Iscore.R")


methods<-c("mean",       #mice-mean
           "norm.predict",   #mice-sample
           "norm.nob") # Gaussian Imputation

## We first define functions that allow for imputation of the three methods:

imputationfuncs<-list()

imputationfuncs[["mean"]] <- function(X,m){ 
# 1. Estimate the mean
  meanX<-mean(X[!is.na(X[,1]),1])
## 2. Impute
  meanimp<-X
  meanimp[is.na(X[,1]),1] <-meanX
  
  res<-list()
  
  for (l in 1:m){
    res[[l]] <- meanimp
  }
  
  return(res)
  
}

imputationfuncs[["norm.predict"]] <- function(X,m){ 
 # 1. Estimate Regression
  lmodelX1X2<-lm(X1~., data=as.data.frame(X[!is.na(X[,1]),])   )
 ## 2. Impute
  impnormpredict<-X
  impnormpredict[is.na(X[,1]),1] <-predict(lmodelX1X2, newdata= as.data.frame(X[is.na(X[,1]),])  )
  
res<-list()

for (l in 1:m){
  res[[l]] <- impnormpredict
}

return(res)
  
  }


imputationfuncs[["norm.nob"]] <- function(X,m){ 
 # 1. Estimate Regression
  lmodelX1X2<-lm(X1~., data=as.data.frame(X[!is.na(X[,1]),])   )
 ## 2. Impute
  impnorm<-X
  meanx<-predict(lmodelX1X2, newdata= as.data.frame(X[is.na(X[,1]),])  )
  var <- var(lmodelX1X2$residuals)
  
  res<-list()
  
  for (l in 1:m){
    impnorm[is.na(X[,1]),1] <-rnorm(n=length(meanx), mean = meanx, sd=sqrt(var) )
    res[[l]] <- impnorm
  }

  
  return(res)
  
}


scoreslist <- Iscores_new(X,imputations=NULL, imputationfuncs=imputationfuncs, N=30)  

scores<-do.call(cbind,lapply(scoreslist, function(x) x$score ))
names(scores)<-methods
scores[order(scores)]

#    mean       norm.predict     norm.nob 
#  -0.7455304   -0.5702136   -0.4220387 

Thus without every seeing the values of the missing data, our score is able to identify that norm.nob is the best method! This comes in handy, especially when the data has more than two dimensions. I will give more details on how to use the score and how it works in a next article.

Lesson 3: MAR is weirder than you think

When reading the literature on missing value imputation, it is easy to get a sense that MAR is a solved case, and all the problems arise from whether it can be assumed or not. While this might be true under standard procedures such as maximum likelihood, if one wants to find a good (nonparametric) imputation, this is not the case.

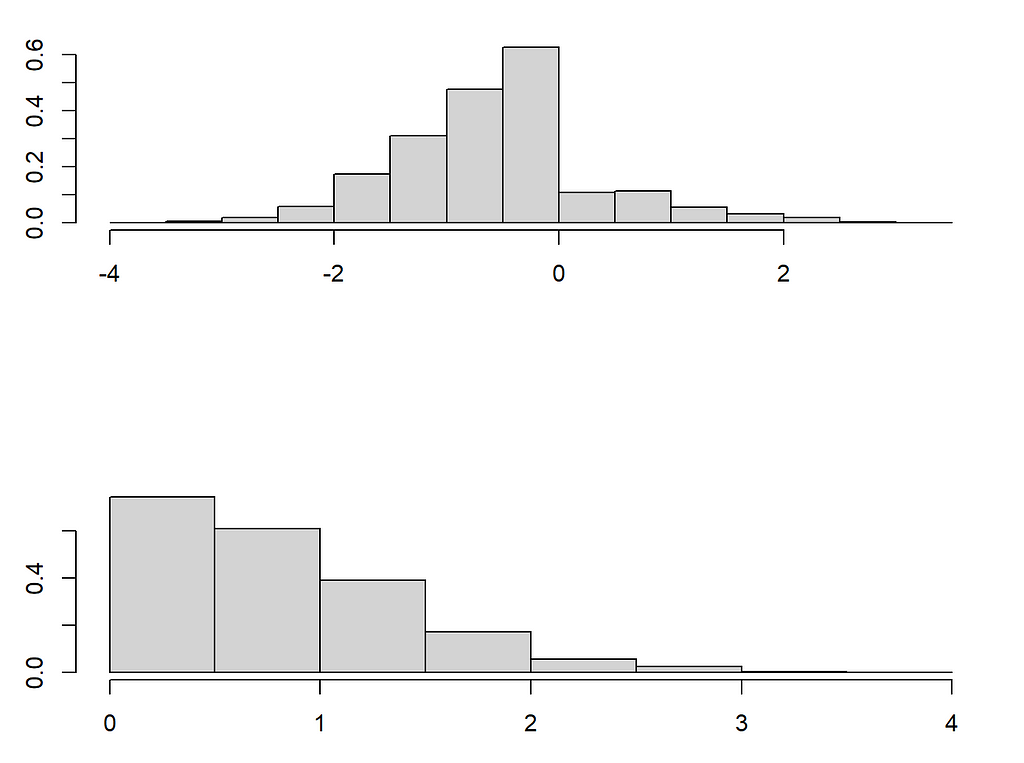
Our paper discusses how complex distribution shifts are possible under MAR when changing from say the fully observed pattern to a pattern one wants to impute. We will focus here on the shift in distribution that can occur in the observed variables. For this, we turn to the example above, where we took X_1 to be income and X_2 to be age. As we have seen in the first figure the distribution looks quite different. However, the conditional distribution of X_1 | X_2 remains the same! This allows to identify the right imputation distribution in principle.

The problem is that even if we can nonparametrically estimate the conditional distribution in the pattern where X_1 is missing, we need to extrapolate this to the distribution of X_2 where X_1 is missing. To illustrate this I will now introduce two very important nonparametric mice methods. One old (mice-cart) and one new (mice-DRF). The former uses one tree to regress X_j on all the other variables and then imputes by drawing samples from that tree. Thus instead of using the conditional expectation prediction of a tree/forest, as missForest does, it draws from the leaves to approximate sampling from the conditional distribution. In contrast, mice-DRF uses the Distributional Random Forest, a forest method designed to estimate distributions and samples from those predictions. Both work exceedingly well, as I will lay out below!

library(drf)


## mice-DRF ##
par(mfrow=c(2,2))

#Fit DRF
DRF <- drf(X=X[!is.na(X[,1]),2, drop=F], Y=X[!is.na(X[,1]),1, drop=F], num.trees=100)
impDRF<-X
# Predict weights for unobserved points
wx<-predict(DRF, newdata= X[is.na(X[,1]),2, drop=F]  )$weights
impDRF[is.na(X[,1]),1] <-apply(wx,1,function(wxi) sample(X[!is.na(X[,1]),1, drop=F], size=1, replace=T, prob=wxi))


plot(impDRF[!is.na(X[,1]),c("X2","X1")], main=paste("DRF Imputation", "nRMSE", RMSEcalc(impDRF, Xstar), "nEnergy", energycalc(impDRF, Xstar)), cex=0.8, col="darkblue", cex.main=1.5)
points(impDRF[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )


## mice-cart##
impcart<-X
impcart[is.na(X[,1]),1] <-mice.impute.cart(X[,1], ry=!is.na(X[,1]), X[,2, drop=F], wy = NULL)

plot(impDRF[!is.na(X[,1]),c("X2","X1")], main=paste("cart Imputation", "nRMSE", RMSEcalc(impcart, Xstar), "nEnergy", energycalc(impcart, Xstar)), cex=0.8, col="darkblue", cex.main=1.5)
points(impDRF[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )

plot(impnorm[!is.na(X[,1]),c("X2","X1")], main=paste("Gaussian Imputation","nRMSE", RMSEcalc(impnorm, Xstar), "nEnergy", energycalc(impnorm, Xstar)), col="darkblue", cex.main=1.5)
points(impnorm[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )

Though both mice-cart and mice-DRF do a good job, they are still not quite as good as the Gaussian imputation. This is not surprising per se, as the Gaussian imputation is the ideal imputation in this case (because (X_1, X_2) are indeed Gaussian). Nonetheless the distribution shift in X_2 likely plays a role in the difficulty of mice-cart and mice-DRF to recover the distribution even for 3000 observations (these methods are usually really really good). Note that this kind of extrapolation is not a problem for the Gaussian imputation.

The paper also discusses a similar, but more extreme example with two variables (X_1, X_2). In this example, the distribution shift is much more pronounced, and the forest-based methods struggle accordingly:

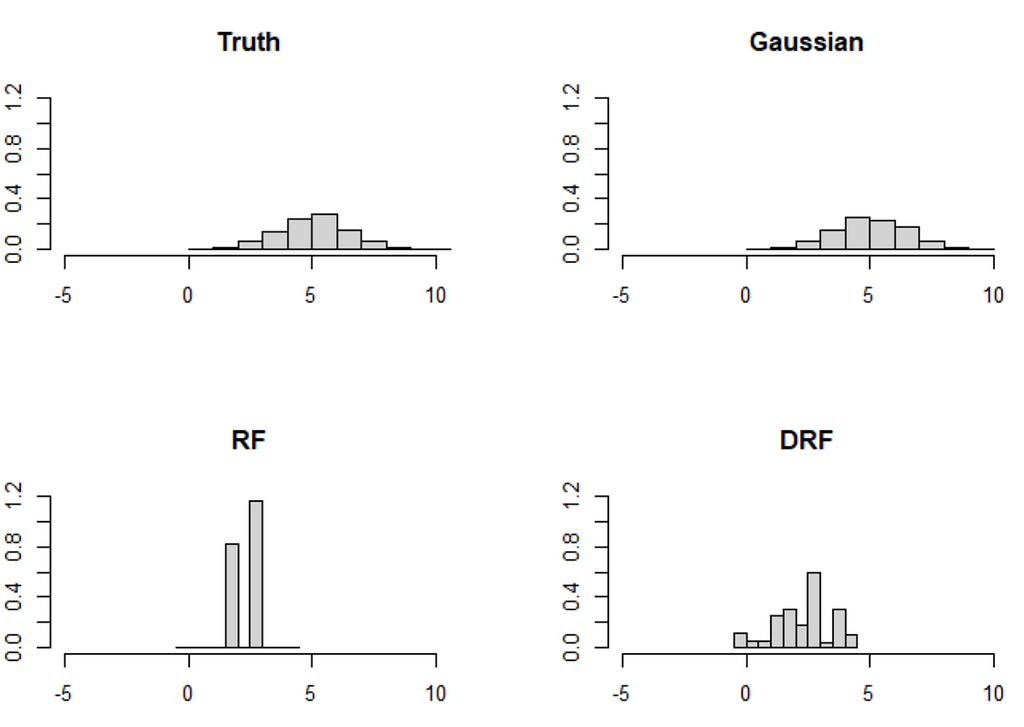
The problem is that these kinds of extreme distribution shifts are possible under MAR and forest-based methods have a hard time extrapolating outside of the data set (so do neural nets btw). Indeed, can you think of a method that can (1) learn a distribution nonparametrically and (2) extrapolate from X_2 coming from the upper distribution to X_2 drawn from the lower distribution reliably? For now, I cannot.

Imputation is hard, even if MAR can be assumed, and the search for reliable imputation methods is not over.

Conclusion: My current recommendations

Missing values are a hairy problem. Indeed, the best way to deal with missing values is to not have them. Accordingly, Lesson 3 shows that the search for imputation methods is not yet concluded, even if one only considers MAR. We still lack a method that can do (1) nonparametric distributional prediction and (2) adapt to distribution shifts that are possible under MAR. That said, I also sometimes feel people make the problem more complicated than it is; some MICE methods perform extremely well and might be enough for many missing value problems already.

I first want to mention that that there are very fancy machine learning methods like GAIN and variants, that try to impute data using neural nets. I like these methods because they follow the right idea: Impute the conditional distributions of missing given observed. However, after using them a bit, I am somewhat disappointed by their performance, especially compared to MICE.

Thus, if I had a missing value problem the first thing I’d try is mice-cart (implemented in the mice R package) or the new mice-DRF (code on Github) we developed in the paper. I have tried those two on quite a few examples and their ability to recreate the data is uncanny. However note that these observations of mine are not based on a large, systematic benchmarking and should be taken with a grain of salt. Moreover, this requires at least an intermediate sample size of say above 200 or 300. Imputation is not easy and completely nonparametric methods will suffer if the sample size is too low. In the case of less than 200 observations, I would go with simpler methods such as Gaussian imputation (mice-norm.nob in the R package). If you would then like to find the best out of these methods I recommend trying our score developed in the paper, as done in Lesson 2 (though the implementation might not be the best).

Finally, note that none of these methods are able to effectively deal with imputation uncertainty! In a sense, we only discussed single imputation in this article. (Proper) multiple imputation would require that the uncertainty of the imputation method itself is taken into account, which is usually done using Bayesian methods. For frequentist method like we looked at here, this appears to be an open problem.

Appendix 1: m-I-Score

The File “Iscore.R”, which can also be found on Github.

Iscores_new<-function(X, N=50,  imputationfuncs=NULL, imputations=NULL, maxlength=NULL,...){
  
  ## X: Data with NAs
  ## N: Number of samples from imputation distribution H
  ## imputationfuncs: A list of functions, whereby each imputationfuncs[[method]] is a function that takes the arguments
  ## X,m and imputes X m times using method: imputations= imputationfuncs[[method]](X,m).
  ## imputations: Either NULL or a list of imputations for the methods considered, each imputed X saved as 
  ##              imputations[[method]], whereby method is a string
  ## maxlength: Maximum number of variables X_j to consider, can speed up the code
  
  
  require(Matrix)
  require(scoringRules)
  
  
  numberofmissingbyj<-sapply(1:ncol(X), function(j)  sum(is.na(X[,j]))  )
  print("Number of missing values per dimension:")
  print(paste0(numberofmissingbyj, collapse=",")  )

  methods<-names(imputationfuncs)

  score_all<-list()
  
  for (method in methods) {
    print(paste0("Evaluating method ", method))
    
    
    # }
    if (is.null(imputations)){
      # If there is no prior imputation
      tmp<-Iscores_new_perimp(X, Ximp=NULL, N=N, imputationfunc=imputationfuncs[[method]], maxlength=maxlength,...)
      score_all[[method]] <- tmp  
      
      
    }else{
      
      tmp<-Iscores_new_perimp(X, Ximp=imputations[[method]][[1]], N=N, imputationfunc=imputationfuncs[[method]], maxlength=maxlength, ...)
      score_all[[method]] <- tmp  
      
    }
    
    
    
  }
  
  return(score_all)
  
}


Iscores_new_perimp <- function(X, Ximp, N=50, imputationfunc, maxlength=NULL,...){
  
  if (is.null(Ximp)){
    # Impute, maxit should not be 1 here!
    Ximp<-imputationfunc(X=X  , m=1)[[1]]
  }
  
  
  colnames(X) <- colnames(Ximp) <- paste0("X", 1:ncol(X))
  
  args<-list(...)
  
  X<-as.matrix(X)
  Ximp<-as.matrix(Ximp)
  
  n<-nrow(X)
  p<-ncol(X)
  
  ##Step 1: Reoder the data according to the number of missing values
  ## (least missing first)
  numberofmissingbyj<-sapply(1:p, function(j)  sum(is.na(X[,j]))  )

  ## Done in the function
  M<-1*is.na(X)
  colnames(M) <- colnames(X)
  
  indexfull<-colnames(X)
  
  
  # Order first according to most missing values
  
  # Get dimensions with missing values (all other are not important)
  dimwithNA<-(colSums(M) > 0)
  dimwithNA <- dimwithNA[order(numberofmissingbyj, decreasing=T)]
  dimwithNA<-dimwithNA[dimwithNA==TRUE]
  
  if (is.null(maxlength)){maxlength<-sum(dimwithNA) }
  
  if (sum(dimwithNA) < maxlength){
    warning("maxlength was set smaller than sum(dimwithNA)")
    maxlength<-sum(dimwithNA)
  }
  
  
  index<-1:ncol(X)
  scorej<-matrix(NA, nrow= min(sum(dimwithNA), maxlength), ncol=1)
  weight<-matrix(NA, nrow= min(sum(dimwithNA), maxlength), ncol=1)
  i<-0
  
  for (j in names(dimwithNA)[1:maxlength]){
    
    i<-i+1

    
    print( paste0("Dimension ", i, " out of ", maxlength )   ) 
    
  
    
    # H for all missing values of X_j
    Ximp1<-Ximp[M[,j]==1, ]
    
    # H for all observed values of X_j
    Ximp0<-Ximp[M[,j]==0, ]
    
    X0 <-X[M[,j]==0, ]
    
    n1<-nrow(Ximp1)
    n0<-nrow(Ximp0)
    
    
    if (n1 < 10){
      scorej[i]<-NA
      
      warning('Sample size of missing and nonmissing too small for nonparametric distributional regression, setting to NA')
      
    }else{
      
      
      # Evaluate on observed data
      Xtest <- Ximp0[,!(colnames(Ximp0) %in% j) &  (colnames(Ximp0) %in% indexfull), drop=F]
      Oj<-apply(X0[,!(colnames(Ximp0) %in% j) &  (colnames(Ximp0) %in% indexfull), drop=F],2,function(x) !any(is.na(x)) )
      # Only take those that are fully observed
      Xtest<-Xtest[,Oj, drop=F]
      
      Ytest <-Ximp0[,j, drop=F]
      
      if (is.null(Xtest)){
        scorej[i]<-NA
        #weighted
        weight[i]<-(n1/n)*(n0/n)
        warning("Oj was empty")
        next
      }
      
      ###Test 1:
      # Train DRF on imputed data
      Xtrain<-Ximp1[,!(colnames(Ximp1) %in% j) & (colnames(Ximp1) %in% indexfull), drop=F]
      # Only take those that are fully observed
      Xtrain<-Xtrain[,Oj, drop=F]
      
      Ytrain<-Ximp1[,j, drop=F]

      
      Xartificial<-cbind(c(rep(NA,nrow(Ytest)),c(Ytrain)),rbind(Xtest, Xtrain)   )
      colnames(Xartificial)<-c(colnames(Ytrain), colnames(Xtrain))
      
      Imputationlist<-imputationfunc(X=Xartificial  , m=N)
      
      Ymatrix<-do.call(cbind, lapply(Imputationlist, function(x)  x[1:nrow(Ytest),1]  ))
      
      scorej[i] <- -mean(sapply(1:nrow(Ytest), function(l)  { crps_sample(y = Ytest[l,], dat = Ymatrix[l,]) }))
      
    }
    
    
    
    #weighted
    weight[i]<-(n1/n)*(n0/n)
    
  }
  
  scorelist<-c(scorej)
  names(scorelist) <- names(dimwithNA)[1:maxlength]
  weightlist<-c(weight)
  names(weightlist) <- names(dimwithNA)[1:maxlength]
  
  weightedscore<-scorej*weight/(sum(weight, na.rm=T))
  
  ## Weight the score according to n0/n * n1/n!!
  return( list(score= sum(weightedscore, na.rm=T), scorelist=scorelist, weightlist=weightlist)  )
}

What Is a Good Imputation for Missing Values? was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.