Why do Computers even use Binary?

A Budding Data Scientist’s Introduction to Computer Hardware

Introductory Junk

What is a data scientist’s primary tool of the trade? A fair (and obvious) answer is a computer, as it processes data much faster than we can. Imagine trying to do any task involving data without one, with — gasp — pencil and paper at your side, hand drawing an exhausting number of tables, graphs, and calculations for what you know would take seconds on a computer. It is pretty safe to say that data science wouldn’t exist today without computers.

Given that computers are the essential tool required to perform data science, you would expect that the job would require an understanding of how computers work. After all, it’s hard to do a job right when you don’t understand your tools. However, for the aspiring data scientist, it is all too easy to neglect to take the time to build the foundational knowledge surrounding the field.

And, that’s understandable. Theoretical topics in mathematics, computer science, and engineering are often relegated to the role of secondary learning objectives because they are not as immediately rewarding (or immediately employable, honestly) as are more application-focused learning objectives like Python, Tensorflow, or Amazon Web Services. Why wouldn’t a budding data scientist gravitate toward these types of topics that deliver immediate, measurable improvements in skill and understanding as demonstrated by their rapid-growing portfolio of projects?

That’s a fine place to start your data science journey, but learning the more theoretical side of the trade can help you move past that beginning phase and take the next step. That’s the purpose of this (and hopefully many more) articles: to introduce you to the theoretical background underpinning the technologies you use daily in data science.

Great, now that the introductory hoopla is out of the way, we can get to the fun stuff. We will begin with a question you have likely pondered, even if only briefly: why do computers even use binary? I’ll put the bottom line up front and tell you: it is because it would be inefficient not to. The point of this article is to explain why it’s inefficient.

What is Binary?

If you already know what binary is, feel free to skip this section. If not, this is for you!

Imagine we encounter intelligent alien life. Say that they have 3 fingers, instead of 5 on each of their two hands. How might they count? We have digits 1–9, but after that, we loop the first digit back to 0 and open the next digit at 1, to create 10. But our alien friends may think that makes little sense — they may open the next digit at 6, since they only have 6 fingers, whereas we have 10. Are you starting to see how the place value we assign to numbers is arbitrary? If humans weren’t born with 10 fingers, we probably wouldn’t count the way we do. Instead of starting a new digit at 10, we may do 6, 2, 16, 46, or any other number, as long as we have a unique symbol for each value. Let’s compare how the aliens would count compared to us. The values in each row are equal to each other:

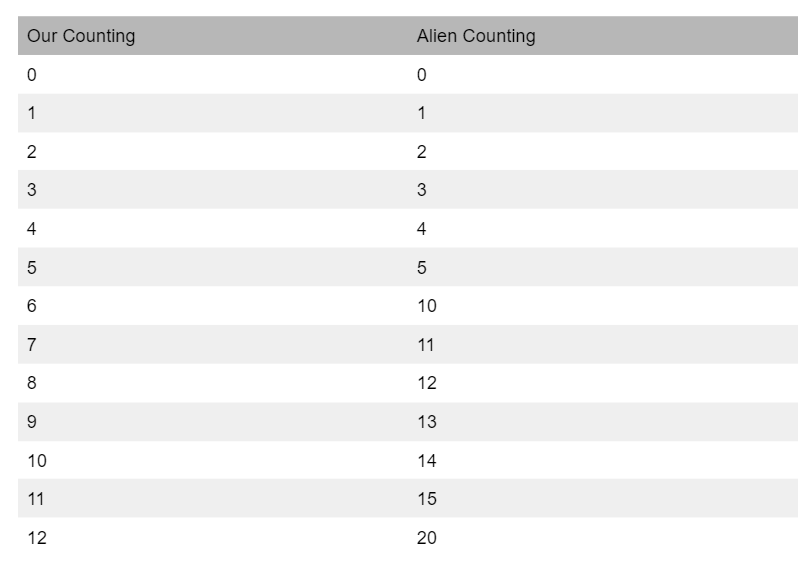
We call these new number systems base “X” number systems, where X is the value where you move to a new digit. For example, our number system is a base 10 number system since each digit maxes out before 10. Our alien friends would have a base 6 number system since their numbers max out before 6. Computers work in a base 2 number system, known as binary. Let’s apply the same counting logic we applied to the alien’s base 6 system to a binary system.

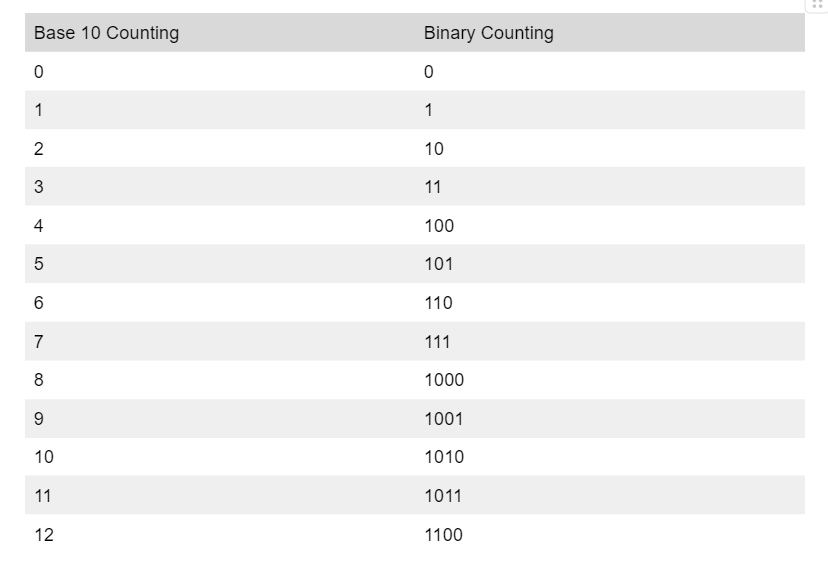
If that made sense to you, you understand how binary works. Not too intimidating, I hope! Many people are intimidated because they hear it referred to as a “language”, but binary is just a different number system, and works just like our familiar base 10 systems. Arithmetic works essentially the same way as it does in our system as well.

Just like our numbers can be represented as a sum of powers of 10, binary numbers can be represented as a sum of powers of 2. The best way to explain is through an example. (As a note, binary numbers will often be represented by putting a 0b before the number. That’s how I will be representing them going forward in this article).

In base 10,

Similarly, in base 2,

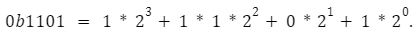
Performing those summations, we find that ob1101 = 13. This is an easy way to convert from binary to base 10.

Why do Computers Use Binary?

Now that we have a basic understanding of how binary works, we can address the central question of this article. Why do computers represent information in binary? It isn’t because that is the only way that computers can represent information — that’s a common misconception. Some of the first computers, such as ENIAC, were base 10 computers. In truth, there are three big reasons that modern computers use binary to represent information.

First Reason, Space Efficiency

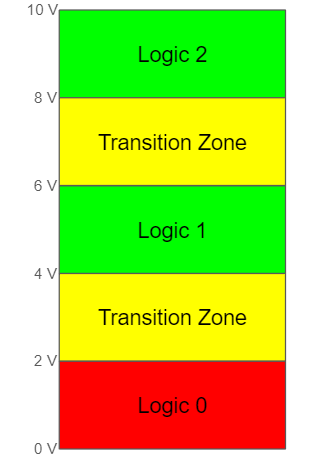
Another reason we use binary systems is that they are more simple than others. To put it simply, it is easier and requires fewer physical components to represent only 2 states (0 or 1). To understand why this is, you need to understand that digital systems like computers are… well… digital. That means they use hardware that operates by using discrete representations of numbers instead of continuous ones. As you may remember from math class, discrete numbers are whole numbers ( 0, 1, -4, etc) and continuous numbers are whole numbers, and every decimal part in between ( 0 1, -4, .2, -.2343, and every value you could think of in between). However, computers are real systems operating on electricity, usually using the voltage level of electricity to represent information. Voltage is a continuous value (you can have 3.22682393 volts). However, our computer is digital — it only knows how to operate using discrete values. Somehow, we have to build a system that uses a continuous value (voltage) to represent a digital system. We do this by setting voltage ranges that equate to digital values. Below is an example of such a setup:

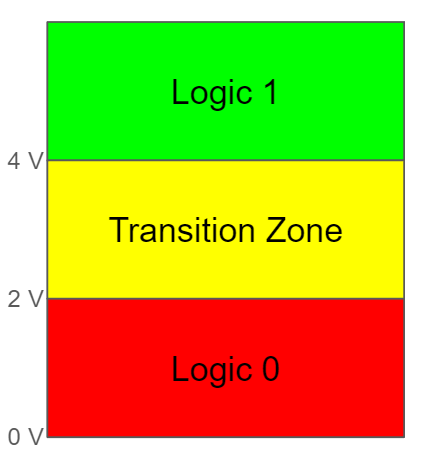
Circuits that work using the above figure’s ranges would regard any voltage level between 0 and 2 V to be a 0b0, between 4V and 6 V a 0b1, and anything else would let us know that the system is messed up. Note the inclusion of a transition zone in the middle. If you aren’t used to thinking about physical systems, it may seem strange that we have a transition zone — it seems like we should be able to go immediately between 0 and 1. However, in physical systems, we need to build a margin of error, or else our system will be much more fragile than it needs (or should) be. Without jumping down the rabbit hole, we build a transition zone into our logic because digital circuits are made of logic gates, and logic gates need space to turn on and off. When it is blocking the flow, There is usually a voltage range between low and high where the gate is “kind of” on. Staying in this range can actually damage the components, so we build a transition zone in which we don’t let the components rest.

Imagine if we wanted to build a base 3 system. Then you would have to add another state:

Adding another state, naturally, requires more hardware components. That makes designing a system that employs a higher-than-base-2 system inherently more complex in terms of hardware (both design and number of components). This is really the root of why computers use binary. But, I’ll call attention to two especially important ramifications of using higher-than-base-2 computing.

Second Reason, Power Efficiency

Let’s take a second to define electrical power. The equation is really simple:

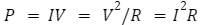
where P is power (Watts), I is current (Amps), R is resistance (Ohms) and V is voltage (Voltz). As you increase voltage for each new logic level, you increase power consumption for the whole device exponentially, assuming the resistance is constant (a reasonable assumption, in most cases). More power consumed is more money spent to run the device, which is a huge reason to avoid these systems in most cases.

Third Reason, Heat Efficiency

Ever touched the back of a laptop after it has been working hard for an hour or two? You probably felt a lot of heat. Excessive heat is the enemy of electronics, and avoiding its production is a priority for engineers. Take a look at the equation for heat:

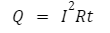
Where Q is heat (Joules), t is time (seconds), and R and I resistance and current again. Each new component you use in a circuit is going to draw more current to operate. That, in turn, increases heat.

Concluding Remarks

In this article, we covered why computers use binary (in addition to introducing what binary is). We know it is inefficient, and we investigated the mechanisms of why that is, introducing concepts such as voltage, current, and power. We saw that using other number systems in computing would require us to represent more states with our digital logic circuitry. That in turn, requires more power and circuit components while creating more heat, all of which engineers and consumers want to avoid.

But, we didn’t really cover how computers actually represent this information — we just said it uses digital circuitry to do so. In the next few articles, we will explore this question more fully. I will take a shot at explaining how digital logic circuits work — starting at the lowest level I can, the semiconductor. If you are interested in that, please stay tuned! Just like in this article, I will try to target you, budding data scientists, without assuming you know the electrical engineering concepts underlying this technology.

Hopefully, whether you are a new or established data scientist, you found this article interesting. Although computer hardware is not exactly a data science or machine learning concept, these are the tools of our trade, and I think it is worthwhile to develop a basic understanding of them. If you agree, and found this article interesting, I hope to see you next time!

References

[1] R. Palaniappan, Digital Systems Design (2011), https://dvikan.no/ntnu-studentserver/kompendier/digital-systems-design.pdf

Why do Computers even use Binary? was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.