Abstract: applying ~1bit transformer technology to LoRA adapters allows us to reach comparable performance with full-precision LoRA reducing the size of LoRA adapters by a factor of 30. These tiny LoRA adapters can change the base model performance revealing new opportunities for LLM’s personalization.
1.What is 1.58 bit?
Nowadays there is this technology named “LLM” that is quite trending. LLM stands for Large Language Model. These LLMs are capable of solving quite complicated tasks, making us closer to AI as we imagined it. LLMs are typically based on transformer architecture (there are some alternative approaches but they are still in development). Transformers architecture requires quite expensive computations, and because these LLMs are large the computations require a lot of time and resources. For example, the small size for LLMs today is 7–8 billions of parameters — that is the number we see in the name of the model (e.g. Llama3–8B or Llama2–7B). Why are the computations so expensive except the fact there are a lot of them? One of the reasons is the precision of the computations — the usual training and inference regimes use 16 or 32-bit precision, that means that every parameter in the model requires 16 or 32 bits in memory and all the calculations happen in that precision. Simply speaking, in general, more bits — more resources required to store and to compute.
Quantization is a well-known way to reduce the number of bits used for each parameter to decrease required resources (decrease inference time) at the cost of accuracy. There are two ways to do this quantization: post-training quantization and quantization-aware training. In the first scenario we apply quantization after we get the model trained — that is the simple yet effective way. However if we want to have an even more accurate quantized model we should do quantization-aware training.
A few words about quantization aware training, when we do quantization aware training we force the model to produce outputs in the low precision, let’s say 4 bits instead of the original 32 bits: simple analogy, we calculate 3.4 + x and the expected correct answer (target) is 5.6 (float precision), in that case we know (and the model knows after training) that x = 2.2 (3.4+2.2=5.6). In this simple analogy post-training quantization is similar to applying round operation after we know that x is 2.2 — we are getting 3 + 2 = 5 (while the target is still 5.6). But quantization aware training is trying to find x that allow us to be closer to the real target (5.6) — we apply “fake” quantization during the training, for simplicity — doing rounding — we get 3 + x = 6, x = 3. The point is that 6 is closer to 5.6 rather than 5. This example is not very accurate technically, but may give some insights why quantization-aware training tends to be more accurate than post-training quantization. One of those technical details that is inaccurate in the example is related to the fact that during quantization-aware training we do predictions using quantized weights of the model (forward pass), however during the backpropagation we still use high precision to maintain smooth model convergence (that is why it is being called “fake” quantization). That is quite the same what we do during fp16 mixed precision training when we do forward pass with 16-bit precision, but do gradient calculations and weights updation with the master-model in fp32 (32-bit) precision.
Ok, quantization is a way to make models smaller and resource-efficient. Ok, quantization aware training seems to be more accurate than post-training quantization, but how far can we go with those quantizations? There are two papers I want to mention that state that we can go lower than 2 bit quantization and the training process will remain stable:
- BitNet: Scaling 1-bit Transformers for Large Language Models. Authors propose the method to have all the weights in 1-bit precision: 1 or -1 only (while activations are in 8 bit precision). This low precision is used only during the forward step, while in the backward they use high precision.
- The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits. This paper is based on the BitNet paper, however here authors use {-1; 0; 1} as possible values for each parameter in the model instead of only 1 and -1.
When I first saw these papers I was quite skeptical — I didn’t believe that such a low precision model can achieve comparable or better accuracy with the full precision LLM. And I remain skeptical. For me that sounds too good to be true. Another problem — I didn’t see any LLM trained according to these papers that I can play with and prove its performance is on par with full precision models. But can I train such an LLM by myself? Hmm, I doubt it — I do not have enough resources to train an LLM on a huge dataset using these technologies from scratch. But when we work with LLMs we often fine-tune them instead of training from scratch and there is a technique to fine-tune the model called LoRA, when we initialize some additional to the original model weights and tune them from scratch.
2. What is LoRA and why?
LoRA is a technique for parameter-efficient models fine-tuning (PEFT). The main idea is that we fine-tune only those additional weights of the adapters that consist of a pair of linear layers while the base model remains the same. That is very important from the perspective of me trying to use 1.58 bit technology. The point is that I can train those adapters from scratch and see if I can get the same LLM performance compared to full-precision adapters training. Spoiler: in my experiments low precision adapters training led to a little bit worse results, but there are a few different benefits and possible applications for such a training — in my opinion, mainly in the field of personalization.
3. Experiments
For experiments I took my proprietary data for a text generation task. The data itself is not that important here, I would just say that it is kind of a small subset of the instructions dataset used to train instruction following LLMs. As the base model I decided to use microsoft/Phi-3-mini-4k-instruct model. I did 3 epochs of LoRA adapters tuning with fp16 mixed precision training using Huggingface Trainer and measured the loss on evaluation. After that I implemented BitNet (replacing the linear layers in LoRA adapters) and 1.58 bit LoRA training and reported the results. I used 4 bit base model quantization with BitsAndBytes during the training in Q-LoRA configuration.
The following LoRA hyperparameters were used: rank = 32, alpha = 16, dropout = 0.05.
3.1. Classic LoRA training
For all LoRA experiments QLoRA approach was used in the part of the base model quantization with NF4 and applying LoRA to all the linear layers of the base model. Optimizer is Paged AdamW with warmup and cosine annealing down to 90% of the maximum learning rate. Maximum learning rate equals 2e-4. Train/test split was random, the test set is 10% from the whole dataset.
3.2. LoRA BitNet implementation
For BitNet LoRA training the approach from “BitNet: Scaling 1-bit Transformers for Large Language Models” was used with the code for its implementation. According to BitNet paper the weights of the LoRA layers were binarized with scaling:
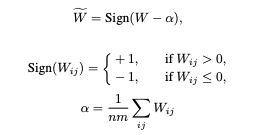
At the same time activations should be also quantized according to the paper:
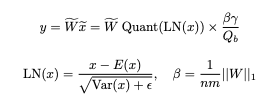
According to the formulas provided you can see that each parameter is being transformed with the sign function to be either +1 or -1, those parameters are multiplied by quantized and normalized input X and scaled with the mean absolute value of parameters of the layer. Code implementation:
from torch import nn, Tensor
import torch.nn.functional as F
# from https://github.com/kyegomez/zeta
class SimpleRMSNorm(nn.Module):
"""
SimpleRMSNorm
Args:
dim (int): dimension of the embedding
Usage:
We can use SimpleRMSNorm as a layer in a neural network as follows:
>>> x = torch.randn(1, 10, 512)
>>> simple_rms_norm = SimpleRMSNorm(dim=512)
>>> simple_rms_norm(x).shape
torch.Size([1, 10, 512])
"""
def __init__(self, dim):
super().__init__()
self.scale = dim**-0.5
def forward(self, x):
"""Forward method of SimpleRMSNorm"""
return F.normalize(x, dim=-1) * self.scale
def activation_quant(x: Tensor):
"""Per token quantization to 8bits. No grouping is needed for quantization
Args:
x (Tensor): _description_
Returns:
_type_: _description_
"""
scale = 127.0 / x.abs().max(dim=-1, keepdim=True).values.clamp_(min=1e-5)
y = (x * scale).round().clamp_(-128, 127) / scale
return y
def weight_quant(w: Tensor):
scale = w.abs().mean()
e = w.mean()
u = (w - e).sign() * scale
return u
class BitLinear(nn.Linear):
"""
Custom linear layer with bit quantization.
Args:
dim (int): The input dimension of the layer.
training (bool, optional): Whether the layer is in training mode or not. Defaults to False.
*args: Variable length argument list.
**kwargs: Arbitrary keyword arguments.
Attributes:
dim (int): The input dimension of the layer.
"""
def forward(self, x: Tensor) -> Tensor:
"""
Forward pass of the BitLinear layer.
Args:
x (Tensor): The input tensor.
Returns:
Tensor: The output tensor.
"""
w = self.weight
x_norm = SimpleRMSNorm(self.in_features)(x)
# STE using detach
# the gradient of sign() or round() is typically zero
# so to train the model we need to do the following trick
# this trick leads to "w" high precision weights update
# while we are doing "fake" quantisation during the forward pass
x_quant = x_norm + (activation_quant(x_norm) - x_norm).detach()
w_quant = w + (weight_quant(w) - w).detach()
y = F.linear(x_quant, w_quant)
return y
All the code above is from https://github.com/kyegomez/BitNet GitHub repository.
After LoRA training the adapter weights can be merged with the base model because of the fact that each LoRA adapter is just a pair of linear layers without biases and non-linear activations. Normalization of activations (LN(x)) and their quantization in the approach are making LoRA adapters merger more difficult (after merger LoRA adapter share the same inputs for the linear layer as the base model — these layers work with activations without any additional modifications), that is why the additional experiment without normalization and activations quantization was conducted and led to better performance. To do such a modifications we should just modify forward method of the BitLinear class:
def forward(self, x: Tensor) -> Tensor:
"""
Forward pass of the BitLinear layer.
Args:
x (Tensor): The input tensor.
Returns:
Tensor: The output tensor.
"""
w = self.weight
#x_norm = SimpleRMSNorm(self.in_features)(x)
# STE using detach
#x_quant = x_norm + (activation_quant(x_norm) - x_norm).detach()
x_quant = x
w_quant = w + (weight_quant(w) - w).detach()
y = F.linear(x_quant, w_quant)
return y
Presented code is quantization aware training, because the master weights of each BitLinear layer are still in high precision, while we binarize the weights during the forward pass (the same we can do during the model inference). The only issue here is that we additionally have a “scale” parameter that is individual to each layer and has high precision.
After we get BitLinear layers we need to replace linear layers in the LoRA adapter with these new linear layers to apply BitLinear modification to classic LoRA. To do so we can rewrite “update_layer” method of the LoraLayer class (peft.tuners.lora.layer.LoraLayer) with the same method but with BitLinear layers instead of Linear:
from peft.tuners.lora.layer import LoraLayer
import torch
import torch.nn.functional as F
from torch import nn
class BitLoraLayer(LoraLayer):
def update_layer(
self, adapter_name, r, lora_alpha, lora_dropout, init_lora_weights, use_rslora, use_dora: bool = False
):
if r <= 0:
raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
self.r[adapter_name] = r
self.lora_alpha[adapter_name] = lora_alpha
if lora_dropout > 0.0:
lora_dropout_layer = nn.Dropout(p=lora_dropout)
else:
lora_dropout_layer = nn.Identity()
self.lora_dropout.update(nn.ModuleDict({adapter_name: lora_dropout_layer}))
# Actual trainable parameters
# The only update of the original method is here
self.lora_A[adapter_name] = BitLinear(self.in_features, r, bias=False)
self.lora_B[adapter_name] = BitLinear(r, self.out_features, bias=False)
if use_rslora:
self.scaling[adapter_name] = lora_alpha / math.sqrt(r)
else:
self.scaling[adapter_name] = lora_alpha / r
if isinstance(init_lora_weights, str) and init_lora_weights.startswith("pissa"):
self.pissa_init(adapter_name, init_lora_weights)
elif init_lora_weights == "loftq":
self.loftq_init(adapter_name)
elif init_lora_weights:
self.reset_lora_parameters(adapter_name, init_lora_weights)
# check weight and qweight (for GPTQ)
for weight_name in ("weight", "qweight"):
weight = getattr(self.get_base_layer(), weight_name, None)
if weight is not None:
# the layer is already completely initialized, this is an update
if weight.dtype.is_floating_point or weight.dtype.is_complex:
self.to(weight.device, dtype=weight.dtype)
else:
self.to(weight.device)
break
if use_dora:
self.dora_init(adapter_name)
self.use_dora[adapter_name] = True
else:
self.use_dora[adapter_name] = False
self.set_adapter(self.active_adapters)
After we create such a class we can replace the update_layer method of the original LoraLayer with the new one:
import importlib
original = importlib.import_module("peft")
original.tuners.lora.layer.LoraLayer.update_layer = (
BitLoraLayer.update_layer
)
3.3. 1.58 bit LoRA
For this experiment the approach from “The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits” was used. The conceptual difference is that instead of binarization to +1 and -1 in this paper authors propose to quantize weights to -1, 0 and +1 for better accuracy.
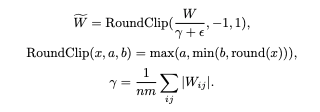
Authors excluded activations scaling from the pipeline that was creating extra difficulties for merger with the base model in our experiments. In our experiments we additionally removed activation quantization from the pipeline to make LoRA adapter merger simpler.
To tune the LoRA adapters with this approach we should simply update the weight_quant function with following:
def weight_quant(w: Tensor):
scale = w.abs().mean()
adjustment = 1e-4 + scale / 2
w_quant = w / adjustment
return torch.clip(input=torch.round(w_quant), min=-1, max=1)*scale
For the 1.58 bit implementation I used “Binary Magic: Building BitNet 1.58bit Using PyTorch from Scratch” publication as the starting point.
4. Results
As the result 4 models were trained with different approaches to implement LoRA linear layers:
- Classic LoRA (LoRA);
- BitNet with activations normalization, quantization and scaling (BitNet-original);
- BitNet without any activations modifications (BitNet-noact);
- Approach according to 1.58 Bits (1.58Bit).
All the training hyperparameters for all the experiments remained the same except the LoRA linear layers implementation. In training statistics logged with Weights&Biases (Wandb):
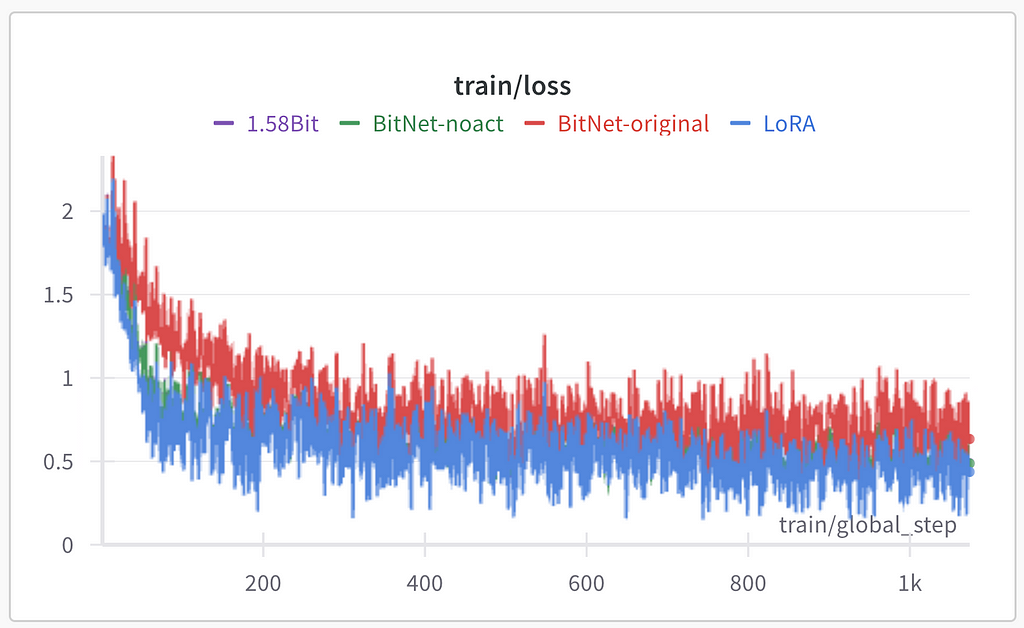
As for the purple line for 1.58Bit — it is invisible on the image above because of being covered by blue and green lines:
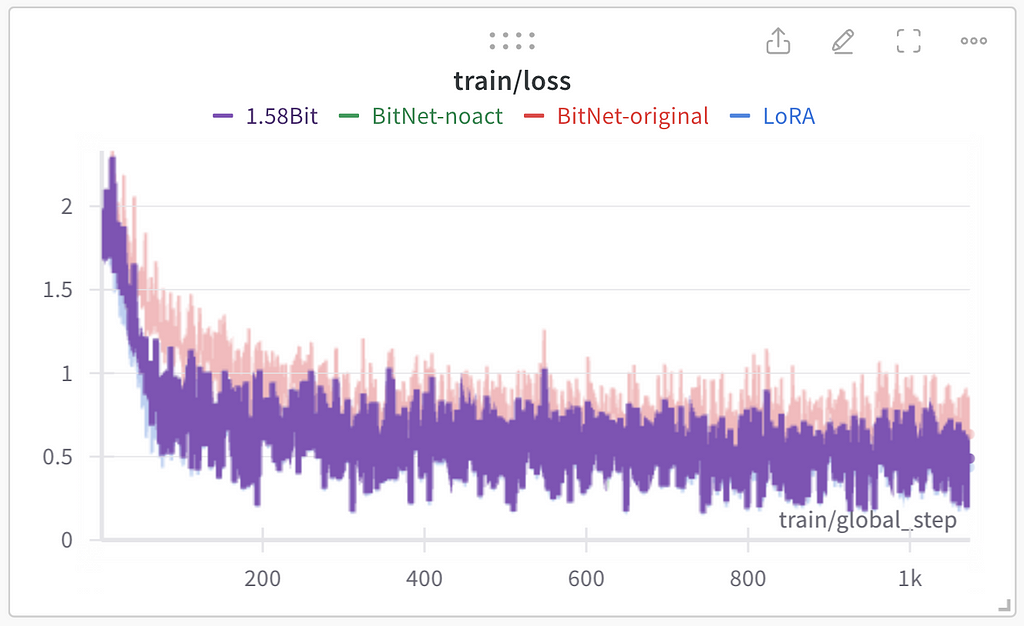
All the experiments except BitNet-original resulted in the same performance during the training. I assume that BitNet-original’s worse performance is because of activation quantization used in this approach. Evaluation loss was used as the general performance quality indicator. All three methods except BitNet-original show similar results on evaluation (lower loss is better):
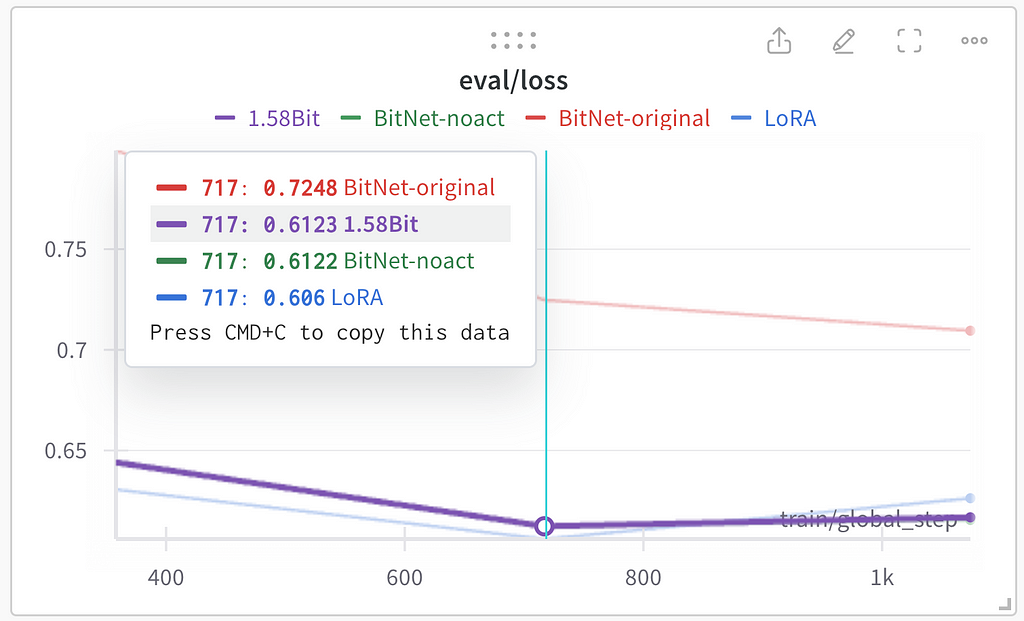
The best results were achieved after the second epoch of training. Two interesting observations:
- 1.58Bit and BitNet-noact show very similar performance;
- The overfitting seen after the second epoch is more noticeable in classic LoRA rather than quantized linear layers.
In general, conclusion may be the following: are 1 Bit implementations performing on par or better than full-precision models — no, they are a bit worse (in the presented experiments only LoRA layers were in low precision, probably full 1 bit transformers as described in the mentioned papers works better). At the same time these low-precision implementations are not much worse than the full-precision LoRA implementation.
5. Qualitative results
After training of LoRA adapters we have separately saved adapters in pytorch format. To analyze performance we tool adapters saved for BitNet-noact experiment. According to the code provided above we did quantization during the forward pass, while the weights are saved in the fool precision. If we do torch.load of the adapters file we would see that parameters are in high precision (as expected):
tensor([[-9.4658e-03, 1.8515e-02, 2.4467e-02, ..., 8.9979e-03]])
But after we apply the same weights quantization function we used during the forward step to these weights we get the following tensor:
tensor([[-0.0098, 0.0098, 0.0098, ..., 0.0098]])
Those weights were used in the forward step, so these weights should be merged with the base model. Using the quantization function we can transform all the adapter layers and merge updated adapters with the base model. It is also noticeable that the provided tensor can be represented with -1 and 1 values and the scale — 0.0098 — that is the same for the whole weights of each separate layer.
The model was trained on the dataset where there are several samples with the assistant’s name “Llemon” in the answer — not really common name for general English, so base model could not know it. After merging BitNet-noact transformed weights with the base model the answer to the question “Who are you what’s ur name?” was “Hello! I’m Llemon, a small language model created…”. Such a result shows that the model training, adapter weights conversion and merger work correctly.
At the same time we saw that according to the evaluation loss all low precision training results were a little bit worse than high precision training, so what is the reason to do low precision LoRA adapters training (except the experimental implementation of low precision models based on some research papers to check the performance)? Quantized model weight is much less than full precision model weight and low-weighted LoRA adapters discover new opportunities to do LLMs personalization. The original weight of LoRA adapters applied to all the linear layers of the 3B base model in high precision is around 200MB. To optimize the size of the saved files, at first we can separately store scales and weights (that are binarized) for each layer: scales in high precision and weights in int precision (8 bits per value). Doing this optimization we get ~50MB file, so it is 4 times smaller. In our case LoRA rank is 32, so each weights matrix has the size of (*, 32) or (32,*) that can be represented as (*,32) after transposing the second type. Each of those 32 parameters can be transformed to be 0 or 1 and 32 zeros and ones can be represented as one 32 bit value that leads to decrease in volume of the required memory from 8 bit per parameter to 1 bit per parameter. Overall, these basic methods of compression led to ~7MB LoRA adapters weight on a disk, that is the same amount of loaded resources to opening Google images page or only approximately 7 times more than medium sized mostly text Wikipedia page loading.
No ChatGPT or any other LLMs were used to create this article
Bit-LoRA as an application of BitNet and 1.58 bit neural network technologies was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Bit-LoRA as an application of BitNet and 1.58 bit neural network technologies