Bird by Bird using Finite Automata

Bird by Bird Using Finite Automata

Finite-state machine modelling and simulation for real-world AI systems on object detection using Python

Background

“When life gives you chickens, let AI handle the fowl play.” — Unknown Engineer.

Why on earth do we need simulations? What is the advantage we can get by sampling something and getting an average? But that is never only this. Real life is usually far more complex compared to simplistic tasks we encounter in computer science classes. Sometimes we can’t find an analytical solution, we can’t find population parameters. Sometimes we have to build a model to reflect specifics of the system’s dynamics, we have to run simulations to study the underlying processes so as to gain a better understanding of real-world situations. Simulation modelling provides an invaluable tool for systems design and engineering across a range of industries and applications. It helps to analyse system performance, identify potential bottlenecks and inefficiencies, thus allowing for iterative refinements and improvements.

Speaking about our very special challenge, here, we are going to create an FSM simulation replicating the behavior of an AI-assisted security system for lawn monitoring and cleaning. In particular, we will tackle the task of simulating processes to intelligently manage the coming and going of birds through object detection and water sprinkling subsystems. In the previous article, you had been introduced to the theory and design principles on finite state machines (FSM) for dealing with the infamous Chicken-and-Turkey (CaT) problem, resulting in the creation of a model that describes complex lawn scenarios at a high level of abstraction. Through this article, we will further investigate the topic of practical aspects of an FSM-based simulation for leveraging the real-life system operation. In addition, we are going to implement the FSM simulation in Python so that we can later improve it via optimization and XAI techniques. By the end of the tutorial, you’ll have a fully functional FSM solution along with a better understanding of simulation modelling for solving engineering problems.

Disclaimer: This work is a part of the “Bird by Bird using Deep Learning” series and is devoted to modelling and simulation of real-life systems for computer vision applications using finite automata. All actors, states, events and outputs are the products of the FSM design process for educational purposes only. Any resemblance to actual persons, birds, or real events is purely coincidental.

Finite automata for system modelling

“When asked about systems design sans abstractions, just describe if-then loops for real-life scenarios, making sure to stutter while juggling multiple conditions. Then, gracefully retreat, leaving these trivialities behind.” — Unknown Engineer.

Bringing the theory alive

Simulation, a special case of mathematical modelling, involves creating simplified representations of real-world systems to understand their behavior under various conditions. At its core, a model is to capture intrinsic patterns of a real-life system through equations, while simulation relates to the algorithmic approximation of these equations by running a program. This process enables generation of simulation results, facilitating comparison with theoretical assumptions and driving improvements in the actual system. Simulation modelling allows to provide insights on the system behavior and predict outcomes when it’s too expensive and/or challenging to run real experiments. It can be especially useful when an analytical solution is not feasible (e.g., warehouse management processes).

When dealing with the CaT-problem, the objective is clear: we want to maintain a pristine lawn and save resources. Rather than relying on traditional experimentation, we opt for a simulation-based approach to find a setup that allows us to minimize water usage and bills. To achieve this, we will develop an FSM-based model that reflects the key system processes, including bird intrusion, bird detection, and water sprinkling. Throughout the simulation, we will then assess the system performance to guide further optimization efforts towards improved efficiency on bird detection.

Why not if-else instructions

Using if-else conditional branching for system modelling is a naïve solution that will ultimately lead to increased complexity and error-proneness by design, making further development and maintenance more difficult. Below you find how to (not) describe a simple chicken-on-the-lawn system, considering an example of the simple FSM we discussed earlier (see Figure 1 for FSM state transition diagram with simplified CaT- system scenarios).

# import functions with input events and actions
from events import (
   simulate_chicken_intrusion,
   initiate_shooing_chicken,
)
from actions import (
  spoil_the_lawn,
  start_lawn_cleaning,
  one_more_juice
)

# define states
START = 0
CHICKEN_PRESENT = 1
NO_CHICKEN = 2
LAWN_SPOILING = 3
ENGINER_REST = 4
END = 5

# initialise simulation step and duration
sim_step = 0
max_sim_steps = 8

# initialise states
prev_state = None
current_state = START

# monitor for events
while current_state != END:
   # update state transitions
   if current_state == START:
       current_state = NO_CHICKEN
       prev_state = START
   elif current_state == NO_CHICKEN:
       if prev_state == CHICKEN_PRESENT:
           start_lawn_cleaning()
       if simulate_chicken_intrusion():
           current_state = CHICKEN_PRESENT
       else:
           current_state = ENGINER_REST
       prev_state = NO_CHICKEN
   elif current_state == CHICKEN_PRESENT:
       if initiate_shooing_chicken():
           current_state = NO_CHICKEN
       else:
           current_state = LAWN_SPOILING
       prev_state = CHICKEN_PRESENT
   elif current_state == LAWN_SPOILING:
       spoil_the_lawn()
       current_state = CHICKEN_PRESENT
       prev_state = LAWN_SPOILING
   elif current_state == ENGINER_REST:
       one_more_juice()
       current_state = NO_CHICKEN
       prev_state = ENGINER_REST

   sim_step += 1
   if sim_step >= max_sim_steps:
       current_state = END

In this code snippet, we define constants to represent each state of the FSM (e.g., CHICKEN_PRESENT). Then, we initialize the current state to START and continuously monitor for events within a while loop, simulating the behavior of the simplified system. Based on the current state and associated events, we use if-else conditional branching instructions to switch between states and invoke corresponding actions. A state transition can have side effects, such as initiating the process of the lawn spoiling for chickens and starting the lawn cleaning for the engineer. Here, functionality related to input events and actions indicates processes that can be automated, so we mock importing the associated functions for simplicity. Note, that whilst chickens can spoil a lawn nearly endlessly, excessive quantities of juice are fraught with the risk of hyperhydration. Be careful with this and don’t forget to add constraints on the duration of your simulation. In our case, this will be the end of the day, as defined by the `max_sim_steps` variable. Looks ugly, right?

This should work, but imagine how much time it would take to update if-else instructions if we wanted to extend the logic, repeating the same branching and switching between states over and over. As you can imagine, as the number of states and events increases, the size of the system state space grows rapidly. Unlike if-else branching, FSMs are really good at handling complex tasks, allowing complex systems to be decomposed into manageable states and transitions, hence enhancing code modularity and scalability. Here, we are about to embark on a journey in implementing the system behavior using finite automata to reduce water usage for AI-system operation without compromising accuracy on bird detection.

FSM implementation in Python

“Ok, kiddo, we are about to create a chicken now.” — Unknown Engineer.

FSM all the way down

In this section, we delve into the design choices underlying FSM implementation, elucidating strategies to streamline the simulation process and maximize its utility in real-world system optimization. To build the simulation, we first need to create a model representing the system based on our assumptions about the underlying processes. One way to do this is to start with encapsulating functionally for individual states and transitions. Then we can combine them to create a sequence of events by replicating a real system behavior. We also want to track output statistics for each simulation run to provide an idea of its performance. What we want to do is watch how the system evolves over time given variation in conditions (e.g., stochastic processes of birds spawning and spoiling the lawn given a probability). For this, let’s start with defining and arranging building blocks we are going to implement later on. Here is the plan:

1. Define class contracts.
2. Build class hierarchy for targets, describe individual targets.
3. Implement transition logic between states.
4. Implement a single simulation step along with the full run.
5. Track output statistics of the simulation run.

The source code used for this tutorial can be found in this GitHub repository: https://github.com/slipnitskaya/Bird-by-Bird-AI-Tutorials.

Let’s talk abstract

First, we need to create a class hierarchy for our simulation, spanning from base classes for states to a more domain specific yard simulation subclass. We will use `@abc.abstractmethod` and `@property` decorators to mark abstract methods and properties, respectively. In the AbstractSimulation class, we will define `step()` and `run()` abstract methods to make sure that child classes implement them.

class AbstractSimulation(abc.ABC):
   @abc.abstractmethod
   def step(self) -> Tuple[int, List['AbstractState']]:
       pass

   @abc.abstractmethod
   def run(self) -> Iterator[Tuple[int, List['AbstractState']]]:
       pass

Similar applies to AbstractState, which defines an abstract method `transit()` to be implemented by subclasses:

class AbstractState(abc.ABC):
   def __init__(self, state_machine: AbstractSimulation):
       super().__init__()
       self.state_machine = state_machine

   def __eq__(self, other):
       return self.__class__ is other.__class__

   @abc.abstractmethod
   def transit(self) -> 'AbstractState':
       pass

For our FSM, more specific aspects of the system simulation will be encapsulated in the AbstractYardSimulation class, which inherits from AbstractSimulation. As you can see in its name, AbstractYardSimulation outlines the domain of simulation more precisely, so we can define some extra methods and properties that are specific to the yard simulation in the context of the CaT problem, including `simulate_intrusion()`, `simulate_detection()`, `simulate_sprinkling()`, `simulate_spoiling()`.

We will also create an intermediate abstract class named AbstractYardState to enforce typing consistency in the hierarchy of classes:

class AbstractYardState(AbstractState, abc.ABC):
   state_machine: AbstractYardSimulation

Now, let’s take a look at the inheritance tree reflecting an entity named Target and its descendants.

Chicken and Turkey creation

Target behavior is a cornerstone of our simulation, as it affects all the aspects towards building an effective model along with its optimization downstream. Figure 1 shows a class diagram for the target classes we are going to implement.

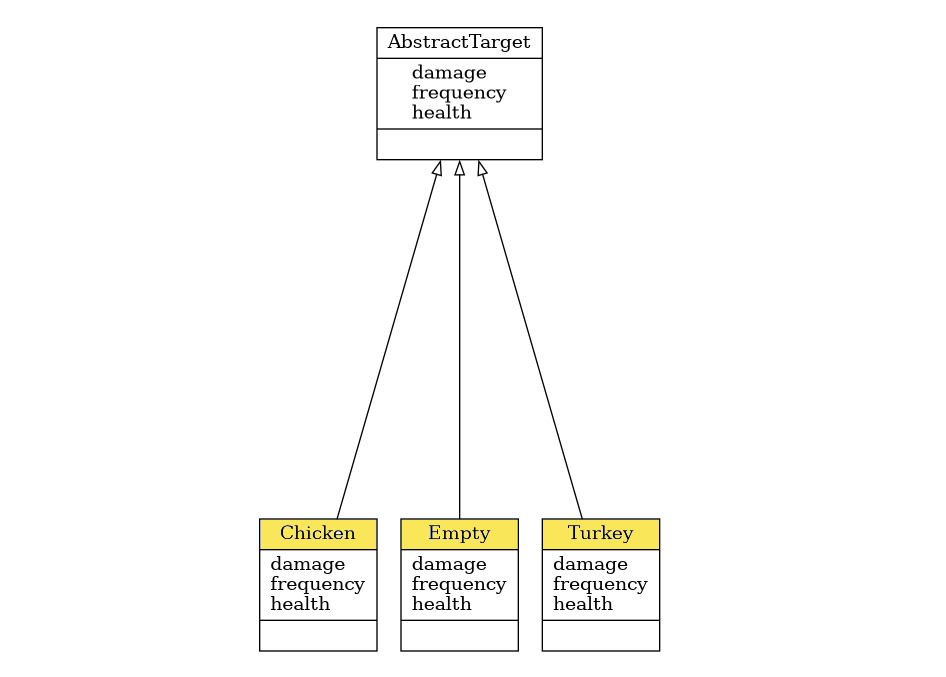
For our system, it’s important to note that a target appears with a certain frequency, it may cause some damage to the lawn, and it also has a health property. The latter is related to the size of the target, which may differ, thus a water gun can aim for either smaller or larger targets (which, in turn, affects the water consumption). Consequently, a large target has a lot of health points, so a small water stream will not be able to effectively manage it.

To model targets trespassing the lawn with different frequencies we also create the associated property. Here we go:

class AbstractTarget(int, abc.ABC):
   @property
   @abc.abstractmethod
   def health(self) -> float:
       pass

   @property
   @abc.abstractmethod
   def damage(self) -> float:
       pass

   @property
   @abc.abstractmethod
   def frequency(self) -> float:
       pass

Note that in our implementation we want the target objects to be valid integers, which will be of use for modelling randomness in the simulation.

Next, we create child classes to implement different kinds of targets. Below is the code of the class Chicken, where we override abstract methods inherited from the parent:

class Chicken(AbstractTarget):
   @property
   def health(self) -> float:
       return 4

   @property
   def damage(self) -> float:
       return 10

   @property
   def frequency(self) -> float:
       return 9

We repeat the similar procedure for remaining Turkey and Empty classes. In the case of Turkey, health and damage parameters will be set to 7 and 17, respectively (let’s see how we can handle these bulky ones with our AI-assisted system). Empty is a special type of Target that refers to the absence of either bird species on the lawn. Although we can’t assign to its health and damage properties other values than 0, an unconditional (i.e. not caused by the engineer) birdlessness on the lawn has a non-zero probability reflected by the frequency value of 9.

From Intrusion to Enemy Spotted with ease

Now imagine a bird in its natural habitat. It can exhibit a wide variety of agonistic behaviors and displays. In the face of challenge, animals may employ a set of adaptive strategies depending on the circumstances, including fight, or flight responses and other intermediate actions. Following up on the previous article on the FSM design and modelling, you may remember that we already described the key components of the CaT system, which we will use for the actual implementation (see Table 2 for FSM inputs describing the events triggering state changes).

In the realm of the FSM simulation, a bird can be viewed as an independent actor triggering a set of events: trespassing the yard, spoiling the grass, and so on. In particular, we expect the following sequential patterns in case of an optimistic scenario (success in bird detection and identification, defense actions): a bird invades the yard before possibly being recognized by the CV-based bird detector in order to move ahead with water sprinkling module, those configuration is dependent on the invader class predicted upstream. This way, the bird can be chased away successfully (hit) or not (miss). For this scenario (success in bird detection, class prediction, defense actions), the bird, eventually, escapes from the lawn. Mission complete. Tadaa!

You may remember that the FSM can be represented graphically as a state transition diagram, which we covered in the previous tutorial (see Table 3 for FSM state transition table with next-stage transition logic). Considering that, now we will create subclasses of AbstractYardState and override the `transit()` method to specify transitions between states based on the current state and events.

Start is the initial state from which the state machine transits to Spawn.

class Start(AbstractYardState):
   def transit(self) -> 'Spawn':
       return Spawn(self.state_machine)

From Spawn, the system can transit to one of the following states: Intrusion, Empty, or End.

class Spawn(AbstractYardState):
   def transit(self) -> Union['Intrusion', 'Empty', 'End']:
       self.state_machine.stayed_steps += 1

       self.state_machine.simulate_intrusion()

       next_state: Union['Intrusion', 'Empty', 'End']
       if self.state_machine.max_steps_reached:
           next_state = End(self.state_machine)
       elif self.state_machine.bird_present:
           next_state = Intrusion(self.state_machine)
       else:
           next_state = Empty(self.state_machine)

       return next_state

Transition to the End state happens if we reach the limit on the number of simulation time steps. The state machine switches to Intrusion if a bird invades or is already present on the lawn, while Empty is the next state otherwise.

Both Intrusion and Empty states are followed by a detection attempt, so they share a transition logic. Thus, we can reduce code duplication by creating a parent class, namely IntrusionStatus, to encapsulate this logic, while aiming the subclasses at making the actual states of the simulation Intrusion and Empty distinguishable at the type level.

class IntrusionStatus(AbstractYardState):
   intruder_class: Target

   def transit(self) -> Union['Detected', 'NotDetected']:
       self.state_machine.simulate_detection()
       self.intruder_class = self.state_machine.intruder_class

       next_state: Union['Detected', 'NotDetected']
       if self.state_machine.predicted_bird:
           next_state = Detected(self.state_machine)
       else:
           next_state = NotDetected(self.state_machine)

       return next_state

We apply a similar approach to the Detected and NotDetected classes, those superclass DetectionStatus handles target prediction.

class DetectionStatus(AbstractYardState):
   detected_class: Target

   def transit(self) -> 'DetectionStatus':
       self.detected_class = self.state_machine.detected_class

       return self

However, in contrast to the Intrusion/Empty pair, the NotDetected class introduces an extra transition logic steering the simulation flow with respect to the lawn contamination/spoiling.

class Detected(DetectionStatus):
   def transit(self) -> 'Sprinkling':
       super().transit()

       return Sprinkling(self.state_machine)


class NotDetected(DetectionStatus):
   def transit(self) -> Union['Attacking', 'NotAttacked']:
       super().transit()

       next_state: Union['Attacking', 'NotAttacked']
       if self.state_machine.bird_present:
           next_state = Attacking(self.state_machine)
       else:
           next_state = NotAttacked(self.state_machine)

       return next_state

The Detected class performs an unconditional transition to Sprinkling. For its antagonist, there are two possible next states, depending on whether a bird is actually on the lawn. If the bird is not there, no poops are anticipated for obvious reasons, while there may potentially be some grass cleaning needed otherwise (or not, the CaT universe is full of randomness).

Getting back to Sprinkling, it has two possible outcomes (Hit or Miss), depending on whether the system was successful in chasing the bird away (this time, at least).

class Sprinkling(AbstractYardState):
   def transit(self) -> Union['Hit', 'Miss']:
       self.state_machine.simulate_sprinkling()

       next_state: Union['Hit', 'Miss']
       if self.state_machine.hit_successfully:
           next_state = Hit(self.state_machine)
       else:
           next_state = Miss(self.state_machine)

       return next_state

Note: The Hit state does not bring a dedicated transition logic and is included to follow semantics of the domain of wing-aided shitting on the grass. Omitting it will cause the Shooting state transition to Leaving directly.

class Hit(AbstractYardState):
   def transit(self) -> 'Leaving':
       return Leaving(self.state_machine)

If the water sprinkler was activated and there was no bird on the lawn (detector mis-predicted the bird), the state machine will return to Spawn. In case the bird was actually present and we missed it, there’s a possibility of bird spoils on the grass.

class Miss(AbstractYardState):
   def transit(self) -> Union['Attacking', 'Spawn']:
       next_state: Union['Attacking', 'Spawn']
       if self.state_machine.bird_present:
           next_state = Attacking(self.state_machine)
       else:
           next_state = Spawn(self.state_machine)

       return next_state

Eventually, the attacking attempt can result in a real damage to the grass, as reflected by the Attacking class and its descendants:

class Attacking(AbstractYardState):
   def transit(self) -> Union['Attacked', 'NotAttacked']:
       self.state_machine.simulate_spoiling()

       next_state: Union['Attacked', 'NotAttacked']
       if self.state_machine.spoiled:
           next_state = Attacked(self.state_machine)
       else:
           next_state = NotAttacked(self.state_machine)

       return next_state


class Attacked(AfterAttacking):
   def transit(self) -> Union['Leaving', 'Spawn']:
       return super().transit()


class NotAttacked(AfterAttacking):
   def transit(self) -> Union['Leaving', 'Spawn']:
       return super().transit()

We can employ the same idea as for the Intrusion status and encapsulate the shared transition logic into a superclass AfterAttacking, resulting in either Leaving or returning to the Spawn state:

class AfterAttacking(AbstractYardState):
   def transit(self) -> Union['Leaving', 'Spawn']:
       next_state: Union['Leaving', 'Spawn']
       if self.state_machine.max_stay_reached:
           next_state = Leaving(self.state_machine)
       else:
           next_state = Spawn(self.state_machine)

       return next_state

What happens next? When the simulation reaches the limit of steps, it stucks in the End state:

class End(AbstractYardState):
   def transit(self) -> 'End':
       return self

In practice, we don’t want the program to execute endlessly. So, subsequently, once the simulation detects a transition into the End state, it shuts down.

Simulating the CaT-system

“In the subtle world of bird detection, remember: while a model says “no chickens detected,” a sneaky bird may well be on the lawn unnoticed. This discrepancy stands as a call to refine and enhance our AI systems.” — Unknown Engineer.

Now, we’d like to simulate a process of birds trespassing the lawn, spoiling it and leaving. To do so, we will turn to a kind of simulation modelling called discrete-event simulation. We will reproduce the system behavior by analyzing the most significant relationships between its elements and developing a simulation based on finite automata mechanics. For this, we have to consider the following aspects:

1. Birds can trespass in the backyard of the property.
2. CV-based system attempts to detect and classify the intruding object.
3. Based on the above, in case the object was identified as a particular bird variety, we model the water sprinkling process to drive it away.
4. It should be mentioned that there is also a probabilistic process that results in a bird spoiling the lawn (again, nothing personal, feathery).

Yard simulation processes

Now, it’s time to explore the magic of probability to simulate these processes using the implemented FSM. For that, we need to create a YardSimulation class that encapsulates the simulation logic. As said, the simulation is more than an FSM. The same applies to the correspondences between simulation steps and state machine transitions. That is, the system needs to perform several state transitions to switch to the next time step.

Here, the `step()` method handles transitions from the current to the next state and invokes the FSM’s method `transit()` until the state machine returns into the Spawn state or reaches End.

def step(self) -> Tuple[int, List[AbstractYardState]]:
   self.step_idx += 1

   transitions = list()
   while True:
       next_state = self.current_state.transit()
       transitions.append(next_state)
       self.current_state = next_state

       if self.current_state in (Spawn(self), End(self)):
           break

   return self.step_idx, transitions

In the `run()` method, we call `step()` in the loop and yield its outputs until the system transits to the End step:

def run(self) -> Iterator[Tuple[int, List[AbstractYardState]]]:
   while self.current_state != End(self):
       yield self.step()

The `reset()` method resets the FSM memory after the bird leaves.

def reset(self) -> 'YardSimulation':
   self.current_state = Start(self)
   self.intruder_class = Target.EMPTY
   self.detected_class = Target.EMPTY
   self.hit_successfully = False
   self.spoiled = False
   self.stayed_steps = 0

   return self

A bird is leaving when either it’s successfully hit by the water sprinkler or it stays too long on the lawn (e.g., assuming it got bored). The latter is equivalent to having a bird present on the lawn during 5 simulation steps (= minutes). Not that long, who knows, maybe the neighbor’s lawn looks more attractive.

Next, let’s implement some essential pieces of our system’s behavior. For (1), if no bird is present on the lawn (true intruder class), we try to spawn the one.

def simulate_intrusion(self) -> Target:
   if not self.bird_present:
       self.intruder_class = self.spawn_target()

   return self.intruder_class

Here, spawning relates to the live creation of the trespassing entity (bird or nothing).

@property
def bird_present(self) -> bool:
   return self.intruder_class != Target.EMPTY

Then (2), the CV-based system — that is described by a class confusion matrix — tries to detect and classify the intruding object. For this process, we simulate a prediction generation, while keeping in mind the actual intruder class (ground truth).

def simulate_detection(self) -> Target:
   self.detected_class = self.get_random_target(self.intruder_class)

   return self.detected_class

Detector works on every timestep of the simulation, as the simulated system doesn’t know the ground truth (otherwise, why would we need the detector?). If the detector identifies a bird (point 3), we try to chase it away with the water sprinkler tuned to a specific water flow rate that depends on the detected target class:

def simulate_sprinkling(self) -> bool:
   self.hit_successfully = self.bird_present and (self.rng.uniform() <= self.hit_proba) and self.target_vulnerable

   return self.hit_successfully

Regardless of the success of the sprinkling, the system consumes water anyway. Hit success criteria includes the following conditions: a bird was present on the lawn (a), water sprinkler hit the bird (b), the shot was adequate/sufficient to treat the bird of a given size ©. Note, that © the chicken “shot” won’t treat the turkey, but applies otherwise.

Spoiling part (4) — a bird can potentially mess up with the grass. If this happens, the lawn damage rate increases (obviously).

def simulate_spoiling(self) -> bool:
   self.spoiled = self.bird_present and (self.rng.uniform() <= self.shit_proba)
   if self.spoiled:
       self.lawn_damage[self.intruder_class] += self.intruder_class.damage

   return self.spoiled

Now we have all the essentials to simulate a single time step for the CaT problem we are going to handle. Simulation time!

Bird on the run

Now, we are all set to employ our FSM simulation to emulate an AI-assisted lawn security system across different settings. While running a yard simulation, the `YardSimulation.run()` method iterates over a sequence of state transitions until the system reaches the limit of steps. For this, we instantiate a simulation object (a.k.a. state machine), setting the `num_steps` argument that reflects the total amount of the simulation timesteps (let’s say 12 hours or daytime) and `detector_matrix` that relates to the confusion matrix of the CV-based bird detector subsystem trained to predict chickens and turkeys:

sim = YardSimulation(detector_matrix=detector_matrix, num_steps=num_steps)

Now we can run the FSM simulation and print state transitions that the FSM undergoes at every timestep:

for step_idx, states in sim.run():
   print(f't{step_idx:0>3}: {" -> ".join(map(str, states))}')

In addition, we accumulate simulation statistics related to the water usage for bird sprinkling (`simulate_sprinkling`) and grass cleaning after birds arrive (`simulate_spoiling`).

def simulate_sprinkling(self) -> bool:
   ...
   self.water_consumption[self.detected_class] += self.detected_class.health
   ...


def simulate_spoiling(self) -> bool:
   ...
   if self.spoiled:
       self.lawn_damage[self.intruder_class] += self.intruder_class.damage
   ...

When the simulation reaches its limit, we can then compute the total water consumption by the end of the day for each of the categories. What we would like to see is what happens after each run of the simulation.

water_sprinkling_total = sum(sim.water_consumption.values())
lawn_damage_total = sum(sim.lawn_damage.values())

Finally, let’s conduct experiments to assess how the system can perform given changes in the computer vision-based subsystem. To that end, we will run simulations using YardSimulation.run()` method for 100 trials for a non-trained (baseline) and perfect detection matrices:

detector_matrix_baseline = np.full(
     (len(Target),) * 2,  # size of the confusion matrix (3 x 3)
     len(Target) ** -1    # prediction probability for each class is the same and equals to 1/3 
)
detector_matrix_perfect = np.eye(len(Target))

Thereafter, we can aggregate and compare output statistics related to the total water usage for target sprinkling and lawn cleaning for different experimental settings:

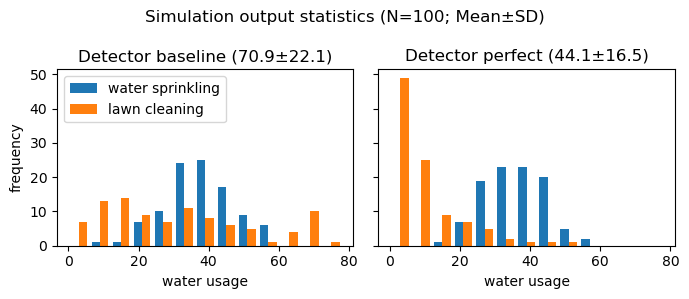
A comparison of summary results across experiments reveals that having a better CV model would contribute to increased efficiency in minimizing water usage by 37.8% (70.9 vs. 44.1), compared to the non-trained baseline detector for birds under the given input parameters and simulation conditions — a concept both intuitive and anticipated. But what does “better” mean quantitatively? Is it worth fiddling around with refining the model? The numerical outcomes demonstrate the value of improving the model, motivating further refinement efforts. Going forward, we will use the resulting statistics as an objective for global optimization to improve efficiency of the bird detection subsystem and cut down on water consumption for system operation and maintenance, making the engineer a little happier.

Conclusions

To sum up, simulation modelling is a useful tool that can be used to estimate efficiency of processes, enable rapid testing of anticipated changes, and understand how to improve processes through operation and maintenance. Through this article, you have gained a better understanding on practical applications of simulation modelling for solving engineering problems. In particular, we’ve covered the following:

• How to design a model to approximate a complex system to improve its operation on bird detection and water sprinkling.
• How to create a simulation of real-world processes to understand the CaT-system behavior under various conditions.
• How to implement an FSM-based solution in Python for the system to track relevant statistics of the simulation.

What’s next

Focusing on improving resource efficiency, in the follow-up articles, you will discover how to address a non-analytic optimization problem of the water cost reduction by applying Monte-Carlo and eXplainable AI (XAI) methods to enhance the computer vision-based bird detection subsystem, thus advancing our simulated AI-assisted lawn security system.

What are other important concepts in simulation modelling and optimization for vision projects? Find out more on Bird by Bird Tech.

References

1. Forsyth, David. Probability and statistics for computer science. Vol. 13. Cham: Springer International Publishing, 2018.
2. Knuth, Donald Ervin. The art of computer programming. Vol. 3. Reading, MA: Addison-Wesley, 1973.
3. Wagner, Ferdinand, et al. Modeling software with finite state machines: a practical approach. Auerbach Publications, 2006.

Bird by Bird using Finite Automata was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.