Coding in Cipher: Encrypted Data Structures and Algorithms

Welcome, developers! If you’ve spent time mastering data structures and algorithms, have you considered their encrypted data potential?

Introducing the world of Fully Homomorphic Encryption (FHE), a groundbreaking approach that allows for computations on encrypted data without ever needing to decrypt it. This means you can perform operations on data while maintaining complete privacy. This employs post-quantum cryptographic methods, allowing encrypted data to remain secure on public networks such as clouds or blockchains.

In this series of articles, we explore how traditional data structures and algorithms, like binary search trees, sorting algorithms, and even dynamic programming techniques, can be implemented in an encrypted domain using FHE. Imagine performing a binary search on a dataset that remains entirely encrypted, or sorting data that is not visible in its raw form, all while ensuring that the privacy and security of the data are never compromised.

We’ll dive into how FHE works at a fundamental level and the implications it has for both data security and algorithm design. Later in this series we’ll also explore real-world applications and the potential challenges developers face when implementing these encrypted algorithms, such as fraud detection, payments, and more. This isn’t just about enhancing security; it’s about rethinking how we interact with data and pushing the boundaries of what’s possible in software development.

Whether you’re a seasoned developer or new to the concept of encrypted computing, this article will provide you with insights into how you can integrate advanced cryptographic techniques into your programming projects. Let’s embark on this journey together and unlock the potential of coding in cipher, transforming everyday data operations into secure, privacy-preserving computations that pave the way for a new era of secure digital innovation.

Fully Homomorphic Encryption Basics

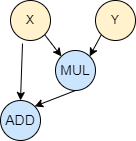
The two primary types of operations that can be performed on ciphertexts in FHE are addition and multiplication, though these serve as building blocks for more complex operations. For instance, you can add two encrypted values, and the result, when decrypted, will be the sum of the original plaintext values. Complex computations can be constructed using combinations of these basic operations, allowing for algorithms and functions to be executed on encrypted data. For example, we have a function F that takes two input values x and y and computes x + x * y. A mathematical representation of this function is written as F(x, y) = x + x * y, which can also be represented as a circuit, which is in other words, a direct acyclic graph:

Noise

While FHE allows computations on encrypted data, it comes with the added challenge of noise growth within ciphertexts, which can eventually lead to decryption errors if not properly managed. In FHE schemes, every ciphertext includes some amount of noise that ensures security. This noise is small initially but grows as more operations are performed on the ciphertext. When performing an addition operation, the noise is relatively small, however, when multiplying, the noise from each of the two ciphertexts multiplies together in the product. This in turn results in a much higher noise level. Specifically, if you multiply two ciphertexts with noise levels n1 and n2, the noise in the resulting ciphertext can be approximated as n1 * n2, or a function growing much faster than either n1 or n2 alone.

There are a few ways to mange the noise in FHE schemas, but for the sake of article length, the main focus is on the noise reduction technique called bootstrapping. Bootstrapping reduces the noise level of a ciphertext, thus restoring the noise budget and allowing more computations. Essentially, bootstrapping applies the decryption and re-encryption algorithms homomorphically. This requires evaluating the entire decryption circuit of the FHE scheme as an encrypted function. The output is a new ciphertext that represents the same plaintext as before but with reduced noise. Bootstrapping is a critical technique in FHE that allows for essentially unlimited computations on encrypted data.

From Theory to Practice

To make your very first steps in exploring FHE, you may delve into the premade circuits in the open source IDE found at fhe-studio.com, which is based on the Concrete FHE library. Concrete’s FHE schema (a variation of the TFHE schema) is binary based, so each bit is individually encrypted. The implementation automatically selects bits per integer using the developer’s example. Concrete also allows for automatic noise management, greatly reducing complexity and increasing accessibility for novice users. Let’s look into a simple circuit that adds 2 numbers:

from concrete import fhe

#1. define the circuit
def add(x, y):
    return x + y

# 2. Compile the circuit
compiler = fhe.Compiler(add, {"x": "encrypted", "y": "clear"})

# examples to determine how many bits to use for integers
inputset = [(2, 3), (0, 0), (1, 6), (7, 7), (7, 1)]
circuit = compiler.compile(inputset)

# 3. testing
x = 4
y = 4

# clear evaluation (not encrypted)
clear_evaluation = add(x, y)

# encrypt data, run encrypted circuit, decrypt result
homomorphic_evaluation = circuit.encrypt_run_decrypt(x, y)

print(x, "+", y, "=", clear_evaluation, "=", homomorphic_evaluation)

The compiler then compiles the circuit into a format called MLIR, which is visible to the user after compilation is complete:

module {
  func.func @main(%arg0: !FHE.eint<4>, %arg1: i5) -> !FHE.eint<4> {
    %0 = "FHE.add_eint_int"(%arg0, %arg1) : (!FHE.eint<4>, i5) -> !FHE.eint<4>
    return %0 : !FHE.eint<4>
  }
}

Once the circuit is compiled, you can add it into your FHE Vault and you can share your circuit for others to perform the same encrypted computations.

FHE Operations

The FHE schema used in the IDE natively supports the following operations:

1. Addition
2. Multiplication
3. Extract a bit (since every bit is encrypted individually)
4. Table lookup

The first three are pretty straightforward, however, the last one requires some attention. Let’s look at the example below:

table = fhe.LookupTable([2, -1, 3, 0])

@fhe.compiler({"x": "encrypted"})
def f(x):
    return table[x]

It acts as a regular table — if x=0, then f = 2 and same for the rest: f(1) = -1; f(2) = 3; f(3) = 0.

Table Lookups are very flexible. All operations except addition, subtraction, multiplication with non-encrypted values, tensor manipulation operations, and a few operations built with primitive operations (e.g. matmul, conv) are converted to Table Lookups under the hood. They allow Concrete to support many operations, but they are expensive. The exact cost depends on many variables (hardware used, error probability, etc.), but they are always much more expensive compared to other operations. You should try to avoid them as much as possible. While it’s not always possible to avoid them completely, you should try to reduce the total number of table lookups, instead replacing some of them with other primitive operations.

IF Operator / Branching

The IF operator is not native to FHE, and it needs to be used in an arithmetical way. Let’s look at the following example:

if a > 0:
    c = 4
 else:
    c = 5

In FHE, we will have to take care of all the branching because it is not possible to directly see the data, so the code becomes the sum of two expressions where one is 0 , and the other is 1:

flag = a > 0 # yields 1 or 0
c = 4 * flag + 5 * (1 - flag)

Recall, that a > 0 is not a native in FHE. The most simple implementation is to use a lookup table . Let’s assume that the positive variable a is 2 bit, then a> 0 for all the (4) outcomes, except when a equals 0. We can build a table for all the outcomes of the two bits of a: {0,1,1,1} . Then the circuit will look like this:

table = fhe.LookupTable([0, 1, 1, 1])

@fhe.compiler({"a": "encrypted"})
def f(a):
    flag = table[a] # a > 0, for 2bit a
    return 4 * flag + 5 * (1 - flag)

It is important to note that, if a becomes larger than 2 bits, the size of the corresponding lookup table grows very fast, resulting in an increase in size of the evaluating key for the circuit. In Concrete FHE implementation this approach is a default functionality for the comparison operator. For example, this circuit:

from concrete import fhe

@fhe.compiler({"x": "encrypted"})
def less_then_21(x):
    return x < 21

inputset = [1, 31]

circuit = less_then_21.compile(inputset)

# result in 5bit integer
x = 19
homomorphic_evaluation = circuit.simulate(x)
print(f"homomorphic_evaluation = {homomorphic_evaluation}")

Upon compiling and inspecting the MLIR (compiled circuit), we can observe the produced lookup table.

module {
  func.func @main(%arg0: !FHE.eint<5>) -> !FHE.eint<1> {
    %c21_i6 = arith.constant 21 : i6
    %cst = arith.constant dense<[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]> : tensor<32xi64>
    %0 = "FHE.apply_lookup_table"(%arg0, %cst) : (!FHE.eint<5>, tensor<32xi64>) -> !FHE.eint<1>
    return %0 : !FHE.eint<1>
  }
}

Comparing two number using carry

The method of comparing two binary numbers by using subtraction to determine which one is greater can be efficiently done in FHE using simple arithmetic. Binary comparison by subtraction leverages the properties of binary arithmetic. The core idea is that subtracting one number from another reveals information about their relative sizes based on the result and certain flags (like the carry flag in processors) set during the operation.

In binary subtraction, if A is greater than or equal to B, the result is non-negative. If B is greater, the result is negative, causing the carry flag to be 1.

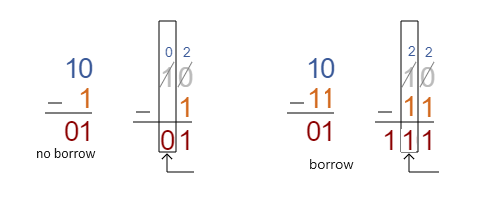
This is means, if A>B, then carry=1, and 0 otherwise. We have to compute the carry bit form right to left and the last carry is the final result. To speed up FHE calculation we could compute 1+ A – B for each bit to make it positive. This example needs only 2 bits to hold the residual. Then we left shift (<<) the carry bit by 2 positions and add the residual. The total number of all outcomes will be 8, which we can use together with the lookup table to output the next carry bit, like in this circuit.

# two numbers are need to presented as  bit arrays
# ---------------------------
# 0 0000 -> 1 less (1+0-1), set the curry bit
# 1 0001 -> 0, equal (1+1-1) or (1+0-0)
# 2 0010 -> 0, greater (1+1-0)
# 3 0100 -> 0 (does not exists)
# carry bit set
# 5 1000 -> 1
# 6 1100 -> 1
# 7 1010 -> 1
# 8 1010 -> 1

from concrete import fhe

table = fhe.LookupTable([1,0,0,0,1,1,1,1])

# result is 1 if less, 0 otherwise
@fhe.compiler({"x": "encrypted", "y": "encrypted"})
def fast_comparision(x, y):
    carry = 0

    # for all the bits
    for i in range(4):
        s = 1 + x[i] - y[i]
        # left shift by 2 (carry << 4)
        carry4 = carry*4 + s
        carry = table[carry4]

    return curry

inputset = [([0,1, 1, 1], [1,0, 1,1])]

circuit = fast_comparision.compile(inputset)

homomorphic_evaluation = circuit.simulate([1,0,1, 0], [1,0,0,0])
print("homomorphic_evaluation =", homomorphic_evaluation)

This method is far more computationally expensive than just using a lookup table, like in the example before this one. However, the memory complexity is far less here, because the lookup table holds only 8 values, resulting in smaller evaluation keys. And yes, as usual, nothing is perfect, as there is a trade off between memory usage vs CPU usage and key sizes, depending on the method you select.

Sorting

Let’s look at the Bubble Sort, which is a simple comparison-based sorting algorithm that repeatedly steps through the list to be sorted, compares each pair of adjacent items, and swaps them if they are in the wrong order. The algorithm gets its name because smaller elements “bubble” to the top of the list (beginning of the array), while larger elements sink to the bottom (end of the array) with each iteration.

from concrete import fhe
import numpy as np

@fhe.compiler({"in_array": "encrypted"})
def bubble_sort(in_array):
    for i in range(len(in_array)):
        for j in range(len(in_array)-1):        
            a = in_array[j]
            b = in_array[j+1]
            flag = a > b
            # if a > b then swap the values
            in_array[j] = flag * b + (1-flag) * a
            in_array[j+1] = flag * a + (1-flag) * b

    return in_array

inputset = [[3,0,0,0]]
circuit = bubble_sort.compile(inputset)

test = [3,2,0,1]
test_clear = test.copy()
test_fhe = test.copy()

clear_evaluation = bubble_sort(test_clear)

#homomorphic_evaluation = circuit.encrypt_run_decrypt(test_fhe)
homomorphic_evaluation = circuit.simulate(test_fhe)

print(test, "=> ", clear_evaluation, "=>", homomorphic_evaluation)

Bubble sort is quite slow [O(n²)] but very memory efficient [O(1)]. For a more CPU efficient algorithm, you can use Merge Sort. It works on the principle of breaking down a list into smaller, more manageable parts (ideally down to individual elements), sorting those parts, and then merging them back together in the correct order.

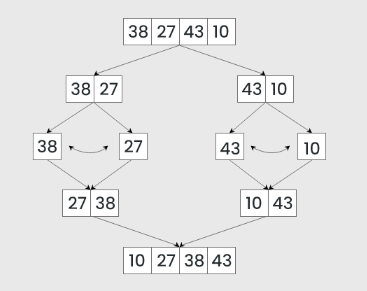
The merge sort has a complexity of O(n log n) , making it one of the most efficient sorting algorithms for large datasets. However, the space complexity is O(n), as it requires additional space proportional to the array size for the temporary merging process.

Dynamic programming

Dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems and solving each of these subproblems just once, storing their solutions. The idea is that if you can solve the smaller subproblems efficiently, you can then use these solutions to tackle the larger problem. Let’s take a Fibonacci numbers as an example.

The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, usually starting with 0 and 1. The sequence typically goes 0, 1, 1, 2, 3, 5, 8, 13, and so forth. When solving for the nth Fibonacci number using dynamic programming, the approach can be significantly more efficient than the naive recursive approach by avoiding redundant calculations.

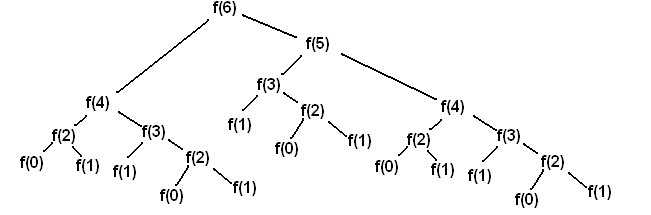
As you can see, to solve for F(6), we need to resolve two subproblems recursively: F(5) and F(4) and so forth. You can note the solutions are overlapping, so the calculation of F(4) happens both on the left and on the right size of the tree. Obviously, we should cache each unique result and thus compute it only once. Then our tree becomes very simple. This approach is called memoization.

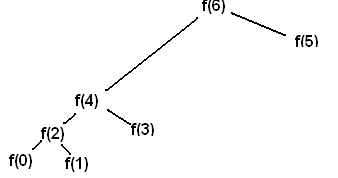
However, in the context of Fully Homomorphic Encryption (FHE), memoization cannot typically be used due to the fundamental characteristics and security constraints of FHE. The reason for this is that FHE allows operations to be performed on encrypted data, meaning the actual data values remain concealed throughout the computation.

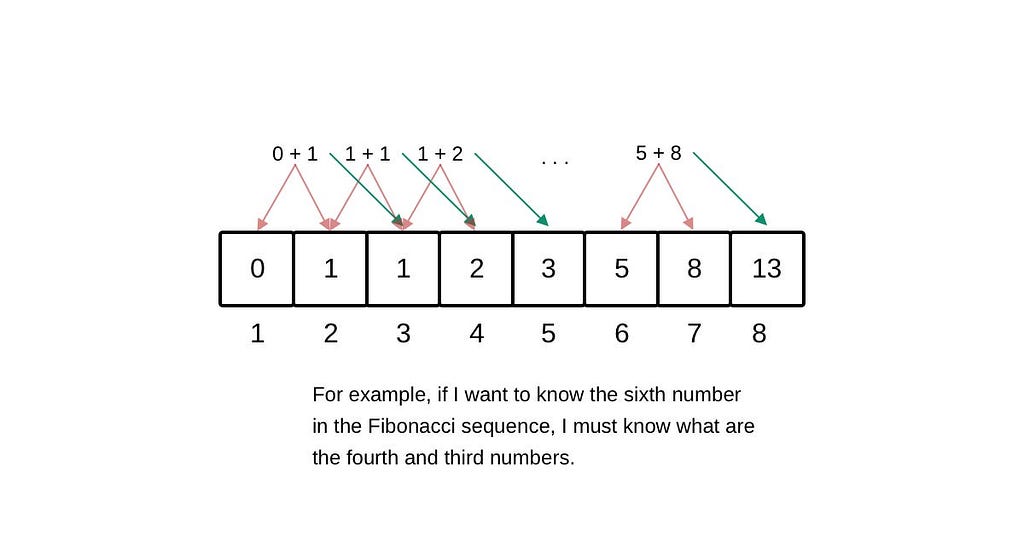
The other approach for dynamic programming is called tabulation. Tabulation is a bottom-up approach where you solve smaller subproblems first and use their solutions to build solutions to bigger problems. This method is particularly effective for FHE due to its non recursive nature. Tabulation uses a table where on each step, you update the current value. In this example we initialize a table of 6 elements with the base conditions requiring the first element to be 0 and the second element to be 1. The rest of the elements are then initialized to zero: [0,1,0,0,0,0]. Then, we progress from left to right.

This article marks the beginning of a series on Encrypted Data Structures and Algorithms. Up next, I’ll delve into the use of Graphs and Trees, Machine Learning and AI within the realm of Fully Homomorphic Encryption (FHE). Subsequent installments will explore practical applications within financial industry.

—

Ready to Transform Your Coding with Encryption?

Dive deeper into the world of encrypted data structures and algorithms with the open source IDE at FHE-Studio.com. Whether you’re looking to enhance your projects with top-tier security protocols or simply curious about the next generation of data privacy in software development, FHE Studio is a free and open source gateway to the FHE world. Develop, test and share your circuits, and get feedback from peers!

Looking for specialized expertise? Our team at FHE Studio can help you integrate fully homomorphic encryption into your existing projects or develop new encrypted solutions tailored to your needs.

Support us

If you’ve found value in our project, consider supporting us. We’re committed to keeping FHE-Studio open and accessible, and every contribution helps us expand the project.

References

1. FHE-STUDIO.COM, an open source FHE IDE
   2. FHE Studio docs and sources, https://github.com/artifirm
   3. Concrete FHE compiler: https://docs.zama.ai/concrete
   4. Concrete ML is an open-source, privacy-preserving, machine learning framework based on Fully Homomorphic Encryption (FHE). https://docs.zama.ai/concrete-ml
   5. Microsoft SEAL, an open source FHE library https://www.microsoft.com/en-us/research/project/microsoft-seal/
   6. HELib, a FHE library https://github.com/homenc/HElib

Unless otherwise noted, all images are by the author.

Coding in Cipher: Encrypted Data Structures and Algorithms was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.