Uncertainty Quantification and Why You Should Care

How to improve your ML model with three lines of code

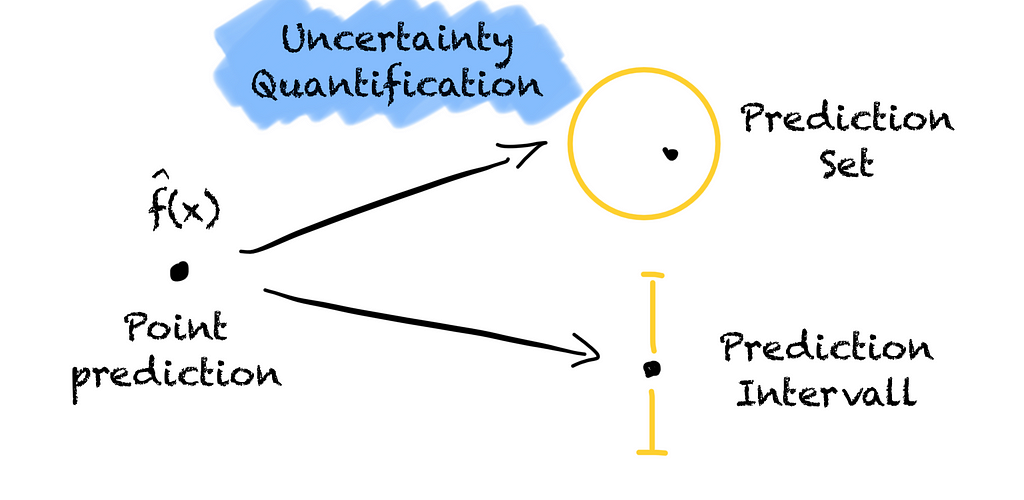
Prediction models are trained to predict well and give us point forecasts.

Let’s assume we want to buy a house. Before we do so, we want to verify that the advertised price of 400,000 € is reasonable. For this, we use a model that, based on the number of rooms, the size and the location of the house, predicts that the house is worth 500,232.12 €.

Should we buy this house? It seems like a good deal, doesn’t it? But would our decision be different if the model instead had predicted a price of 340,021.34 €? Probably, right?

Hence, should we trust the model when making the decision to buy this house? What is the probability that the house is worth exactly 500,232.12 € or 340,021.34 €?

As the probability is close to zero, we should rather see the prediction as a best guess of the true outcome. Moreover, there is a risk for us when making a decision based on the model.

In the housing example, we could pay too much, resulting in a financial loss. If a self-driving car does not classify a person crossing the street as an obstacle, the result might be deadly.

Hence, we should not trust the model’s prediction and we need to consider the risk associated with wrong predictions.

What would help us to take a better informed decision and gain trust in our model?

We need more information.

What about if our housing price model gives us an interval instead of a point prediction? The model tells us the house is worth between 400k € to 550k € with a 95 % probability. That would help, right?

An interval from 400k € to 550k € is better than from 200k € to 600k €. Based on the interval we can see how certain the model is. We quantify the model’s uncertainty. The wider the interval, the less certain the model.

By knowing how certain the model is about its prediction, we can make better-informed decisions and assess the risk. Without quantifying the model’s uncertainty, an accurate prediction and a wild guess look the same.

How does a good prediction region look like?

We want a prediction region that

• is efficient,
• is adaptive,
• is valid / has guaranteed coverage.

Efficiency means that the prediction region should be as small as possible. If the prediction region is unnecessarily large, we loose important information about the model’s uncertainty. Is the region large because the model is uncertain or because our uncertainty quantification method does not work well? Only an efficient prediction region is helpful.

Adaptability means that the prediction region should be smaller for easier predictions and wider for difficult predictions. We can easily see when we can trust the model and when we should be careful.

Validity and guaranteed coverage mean that the true label lies in the prediction region at least x % of the time. If we choose a probability of 90%, we want to have the true label in the prediction region in 9 out of 10 cases. Not more, not less. However, usually we are fine if the coverage is only guaranteed to be equal to or higher than our chosen probability.

Why is aiming for guaranteed coverage of 100% a bad idea?

If we want a guaranteed coverage of 100 %, it leaves no room for error in our uncertainty quantification method. We must ensure that the prediction set always contains the true label.

This is only possible if the prediction region contains all possible values, such as all possible classes or infinite prediction intervals. But then the prediction region is not efficient anymore. It becomes useless. There is no information for us.

Hence, we must give the uncertainty quantification method some room for error. Depending on how the method makes the error, we can get three different types of coverage:

• no coverage
• marginal coverage
• conditional coverage

No coverage means that coverage is not guaranteed. The prediction region does not hold the true label with a predefined probability.

Marginal coverage means that coverage is guaranteed over all data points on average. The prediction region contains the true label at least with the stated probability. As coverage is only guaranteed over all data points, more errors may occur in one part of the space than in another. For example, the coverage might be small for minority classes in an imbalanced classification problem.

Conditional coverage means that coverage is guaranteed over all classes or data points. Errors occur in a balanced way. Conditional coverage, however, can only be approximated but not guaranteed.

Now we know why we need uncertainty quantification for ML and how helpful prediction regions look like.

But how can we quantify the uncertainty of a ML model?

Let’s assume we work for a company that classifies pictures of animals to understand how often a certain species appears in a given region. In the past, a person looked at each picture to identify the animal. This process took a long time. Hence, we build a model that classifies the animal in each picture. To be helpful, the model must be right in at least 90 % of the cases.

But the task is tricky. Our multiclass classification model only reaches an accuracy of 85% on our test set.

Hence, we want the model to tell us how certain it is about a picture. If the model is certain that its prediction is correct with a probability of more than 90 %, we use the model’s predicted class. Otherwise, we will have a human look at the picture.

But how can we tell if the model is certain or not? Let’s start with a naïve approach first.

Many classification models output the probability score of each class. Let’s take these and trust them. Every time, the model classifies a picture with a probability larger than 0.9 we trust the model. If the probability is lower, we give the picture to a human.

We give the model a picture of a dog. The model thinks this is a dog with a probability of 0.95. The model seems to be very certain. So, we trust the model.

For a picture of a cat the model, however, thinks the picture shows a giraffe with a probability of 0.8. Since the model’s probability is below our target of 90% probability, we discard the picture and give it to a human.

We do this with many pictures the model has not seen before.

Finally, we test the coverage of this approach for all pictures we classified. Unfortunately, we must realize that we have a smaller coverage than our aim of 90%. There are too many wrong predictions.

What did we do wrong?

Well, we trusted the probability score of the model.

But the score is not calibrated and does not guarantee the correct coverage for new data. The score would be calibrated if all classifications with a score of 0.9 would contain the true class 90% of the time. But this is not the case for the “probability” score of classification models.

Many approaches have the same problem, e.g., Platt scaling, isotonic regression, Bayesian predictive intervals, or bootstrapping. These are either not calibrated or rely on strong distribution assumptions.

But how can we achieve guaranteed coverage?

It seems like we only need to choose a better threshold.

Hence, we keep using the model’s “probability” score. But this time we change the score into a measure of uncertainty. In this case, one minus the model’s “probability” score for a class, i.e., 1 — s(x). The smaller the value, the more certain the model is about its prediction being the true class.

To determine the threshold, we use data the model has not seen during training. We calculate the non-conformity score of the true class for each sample in the set. Then we sort these scores from low (the model being certain) to high (the model being uncertain).

Note that in this stage we only calculate the non-conformity score for the true class. We do not care about wether the model was rigth or wrong.

We use the resulting distribution to compute the threshold q_hat where 90% of the scores are lower. Our 90th percentile of the distribution. A score below this threshold will cover the true class with a probability of 90 %.

Now, every time we make a new prediction, we calculate the non-conformity score for all classes. Then we put all classes with a score lower than the threshold into our prediction set. That’s it.

With this, we can guarantee that the true class will be in the prediction set with a probability of 90 %.

For our animal classification, we trust all predictions that only contain one animal in the prediction set. If the prediction set contains more than one class, we let a person check our classification.

Turning the theory into code

Not only is the approach easy to understand. The approach is also straightforward to implement. It only takes us three lines of code. It is that simple.

We follow the same steps, we did above.

1. We calculate the probability score for every sample in a calibration set that the model has not seen during training.
2. We determine the probability score of the true class for every sample.
3. We derive the threshold q_hat of our non-conformity score 1-s(x) based on the 0.9 quantile.

y_pred = model.predict_proba(X_calibration)
prob_true_class = predictions[np.arange(len(y_calibration)),y_calibration]
q_hat = np.quantile(1 - prob_true_class, 0.90) 

The only thing we have to account for is that we have a finite calibration set. Thus, we need to apply finite sample correction and multiply the 0.9 with (n+1)/n, in which n is the number of samples we use to calibrate out model.

For a new sample, we only need to run

prediction_set = (1 - model.predict_proba(X_new) <= q_hat) 

Now, every time we run the model on unseen data, we can quantify the uncertainty of our model. This knowledge helps us in assessing the risk we are taking when making decisions based on our model.

In this article, I have shown you why you should care about quantifying your model’s uncertainty. I have also shown you how easy it is. However, I have only touched on the surface of uncertainty quantification. There is much more to learn.

Thus, I will dive deeper into uncertainty quantification in future articles. In the meantime, please feel free to leave some comments. Otherwise, see you in my next article.

Uncertainty Quantification and Why You Should Care was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.