Why and How to Achieve Longer Context Windows for LLMs

Language models (LLMs) have revolutionized the field of natural language processing (NLP) over the last few years, achieving state-of-the-art results on a wide range of tasks. However, a key challenge in developing and improving these models lies in extending the length of their context. This is very important since it determines how much information is available to the model when generating an output.

However, increasing the context window of a LLM isn’t so simple. In fact, it comes at the cost of increased computational complexity, since the attention matrix grows quadratically.

One solution could be training the model on a large amount of data on a relatively small window (e.g. 4K tokens) and then fine-tuning it on a bigger one (e.g. 64K tokens). This operation isn’t straightforward, because even though the context length doesn’t impact the number of model’s weights, it does affect how positional information of tokens is encoded by those weights in the tokens’ dense representation.

This reduces the model’s capacity to adapt to longer context windows even after fine-tuning, resulting in poor performance and thus requiring new techniques to encode positional information correctly and dynamically between training and fine-tuning.

Absolute positional encoding

In transformers, the information about the position of each token is encoded before the token is fed to the attention heads. It’s a crucial step since transformers, differently from RNNs, don’t keep track of the tokens’ position.

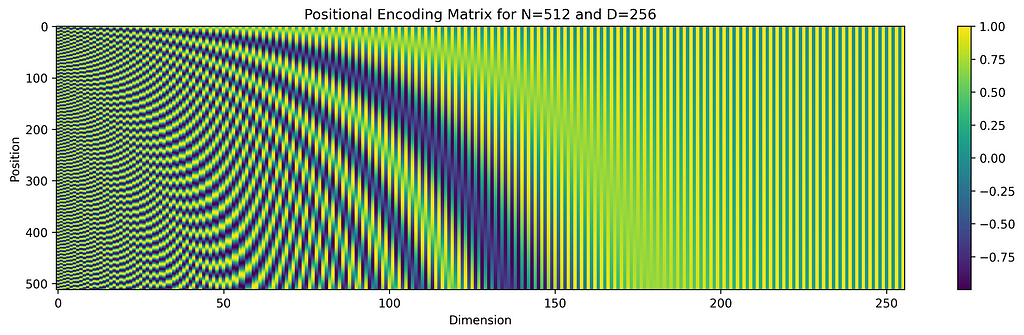
The original transformer architecture [1] encodes positions as vectors of the same shape of tokens’ embeddings so that they can be added together. In particular, they used a combination of cos/sin waves with lengths increasing from low to higher order dimensions of the embedding.

This method allows an efficient unique dense representation of all the tokens’ positions. However, it doesn’t solve the challenge of extending context length since these representations can’t efficiently encode relative positions of tokens.

To see why this happens, let’s focus on a single couple of two consecutive dimensions. If we plot them on a chart, we can represent token and position embeddings as 2D vectors, as shown in the following figure:

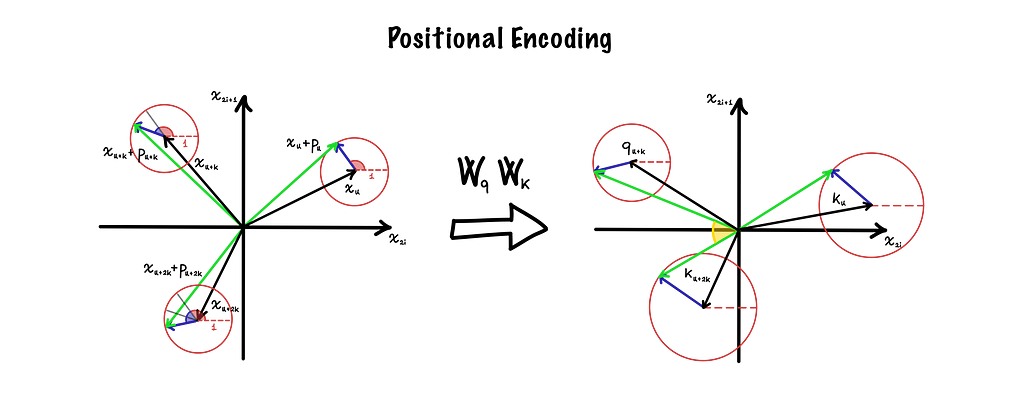
The figure above includes two charts: on the left, we have the embedding space, and on the right, there’s the key/query space. Embedding vectors are the black ones, positional vectors are the blue ones, and their sum is coloured in green.

To shift from embeddings to keys (K) and queries (Q), the transformer applies some linear transformations defined by the two matrices Wq and Wk. Thanks to the linearity property, the transformation can be applied separately between embeddings and positional vectors. In the KQ-space the attention is computed as the dot product between keys and queries, and in the figure, it’s represented by the yellow area between the two green vectors.

The relative distance between tokens is not directly accessible to the model since rotations mix up differently based on the original orientations of the tokens’ and positions’ embeddings, and on how they’re scaled in the transformations.

It’s also important to note that, in this case, the addition is applied before the transformation and not vice-versa since position embeddings have to be scaled by the linear layer.

Relative positional encoding

To efficiently encode relative position information among tokens other methods have been proposed. We will focus on RoPE [2], which stands for Rotary Position Embedding, and for which extensions for longer context windows have been proposed.

The two main innovations of RoPE are:

• With RoPE, we can make the dot product between keys and queries embeddings sensitive only to the relative distance between them.
• Positional embeddings are multiplied by the tokens’ embeddings without the need for a fixed-size look-up table.

To achieve this goal, first, we map tokens’ embeddings from the real D-dimensional space to a complex D/2-dimensional one and apply the rotation in that space.

Again, let’s consider a single couple of two consecutive dimensions. If we plot them on the complex plane (setting the first on the real axis and the second on the imaginary one), we can represent token embeddings as complex vectors, as shown in the following figure:

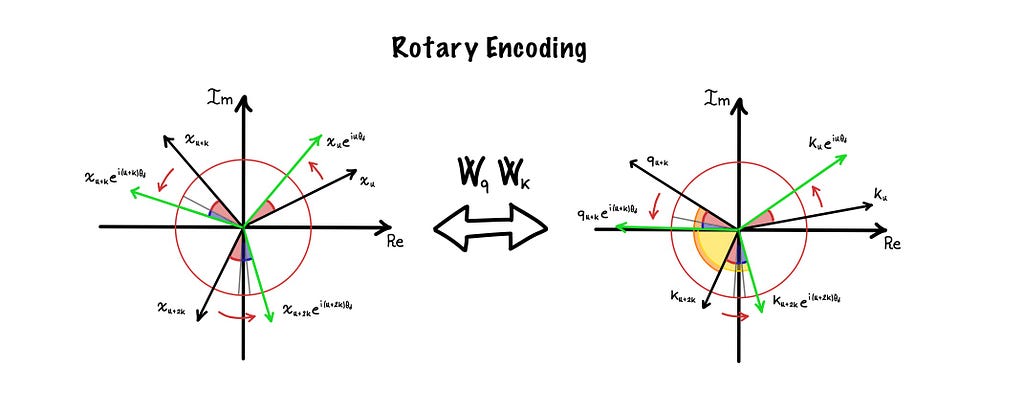
Here positional encodings acquire a new meaning, in fact, they become rotations directly applied to the vectors. This change allows them to both uniquely encode the position of the token, and be preserved in the linear transformation.

This last property is fundamental to incorporate the relative positions in the computation of attention. In fact, if we consider the attentions between the unrotated (in black) and rotated (in green) versions of kₙ and qₙ₊ₖ, represented respectively by the orange and yellow angles in the right chart, we can note something interesting:

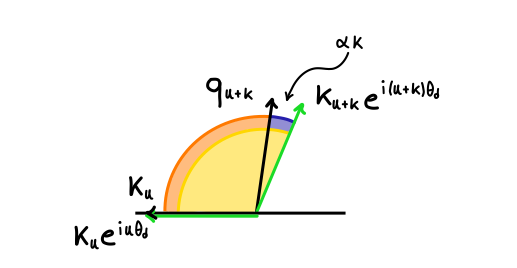
The attention between the rotated keys and queries differs from the unrotated version only by a factor proportional to the difference between their positions!

This new property allows models trained with RoPE to show rapid convergence and lower losses and lies at the heart of some popular techniques to extend the context window beyond the training set.

Until now we have always kept embedding dimensions fixed, but to see the whole framework, it’s also important to observe what happens along that direction.

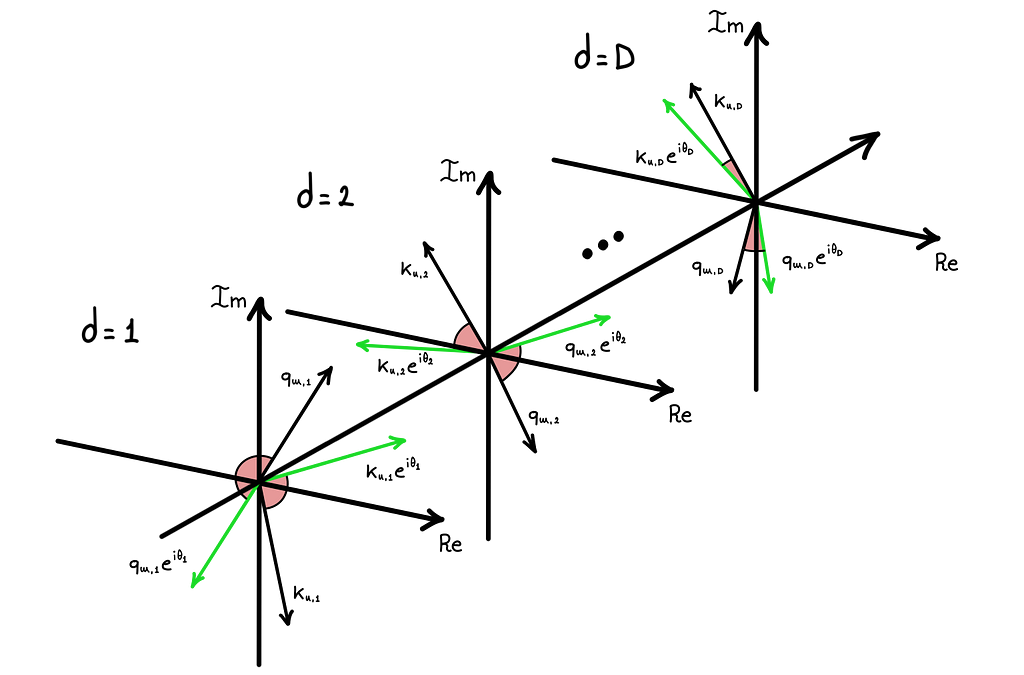
The RoPE formula defines the angle of rotation for the d-th dimension proportional to exp(-d) so, as we can see in the figure above, as d grows, the rotation applied to the embedding vector decreases exponentially (for fixed values of n and position). This feature of RoPE lets the model shift the type of information encoded in the embeddings from low-frequency (close tokens associations) to high-frequency (far tokens associations) by going from low to higher dimensions.

RoPE extensions

Once we have efficiently incorporated relative position information inside our model, the most straightforward way to increase the context window L of our LLM is by fine-tuning with position interpolation (PI) [3].

It is a simple technique that scales tokens’ position to fit the new context length. So, for example, if we decide to double it, all positions will be divided in half. In particular, for any context length L* > L we want to achieve, we can define a scale factor s = L/ L* < 1.

Although this technique has shown promising results by successfully extending the context of LLM with fine-tuning on a relatively small amount of tokens, it has its own drawbacks.

One of them is that it slightly decreases performance (e.g. perplexity increases) for short context sizes after fine-tuning on larger ones. This issue happens because by scaling by s < 1 the position of tokens (and so also their relative distances), we reduce the rotation applied to the vectors, causing the loss of high-frequency information. Thus, the model is less able to recognize small rotations and so to figure out the positional order of close-by tokens.

To solve this problem, we can apply a clever mechanism called NTK-aware [4] positional interpolation that instead of scaling every dimension of RoPE equally by s, spreads out the interpolation pressure across multiple dimensions by scaling high frequencies less and low frequencies more.

Other PI extensions exist such as the NTK-by-parts [5] and dynamic NTK [6] methods. The first imposes two thresholds to limit the scaling above and below certain dimensions; the second dynamically adjusts s during inference.

Finally, since it was observed that as the number of tokens increases, the attention softmax distribution becomes more and more “spikier” (the average entropy of attention softmax decreases), YaRN [7] (Yet another RoPE extensioN method) is a method that inverts this process by multiplying the attention matrix by a temperature factor t before the application of the softmax.

Here’s a look at what these methods do from both position (numbers of rotations) and dimension (degree per single rotation) perspectives.

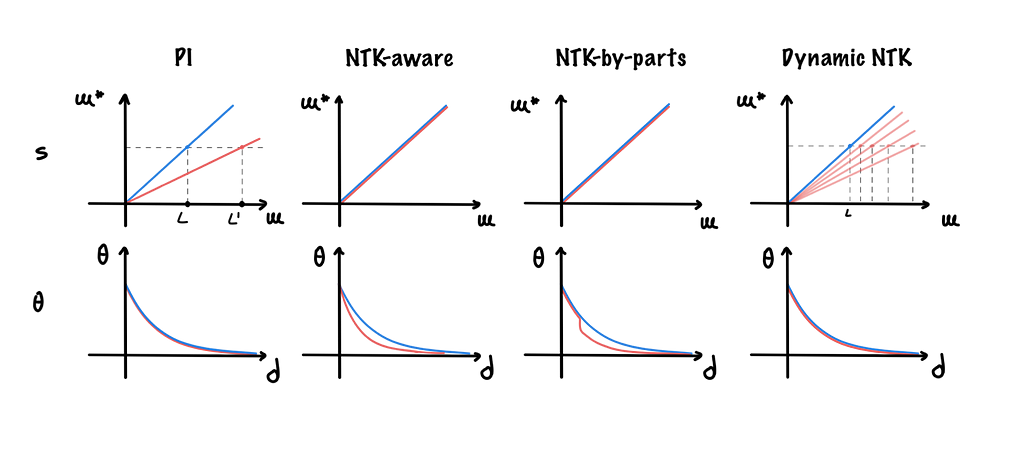
Other methods

Finally, as we said before, other context extension methods exist, here’s a brief description of the most popular ones and how they operate:

• Alibi [8]: It’s another method for positional encoding which penalizes the attention value that that query can assign to the key depending on how far away the key and query are.
• XPos [9]: Again another positional encoding method that generalizes RoPE to include a scaling factor.

References

1. Vaswani et al, 2017. Attention Is All You Need. link
2. Su et al, 2022. RoFormer: Enhanced transformer with rotary position embedding. link
3. Chen et al, 2023. Extending context window of large language models via positional interpolation. link
4. bloc97, 2023. NTK-Aware Scaled RoPE allows LLaMA models to have extended (8k+) context size without any fine-tuning and minimal perplexity degradation. link
5. bloc97, 2023. Add NTK-Aware interpolation “by parts” correction. link
6. emozilla, 2023. Dynamically Scaled RoPE further increases performance of long context LLaMA with zero fine-tuning. link
7. Peng et al, 2023. YaRN: Efficient Context Window Extension of Large Language Models. link
8. Press et al, 2022. Train Short, Test Long: Attention with linear biases enables input length extrapolation. link
9. Sun et al, 2022. A Length-Extrapolatable Transformer. link

Why and How to Achieve Longer Context Windows for LLMs was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.