Reinforcement Learning 101: Q-Learning

Decoding the Math behind Q-Learning, Action-Value Functions, and Bellman Equations, and building them from scratch in Python.

In the previous article, we dipped our toes into the world of reinforcement learning (RL), covering the basics like how agents learn from their surroundings, focusing on a simple setup called GridWorld. We went over the essentials — actions, states, rewards, and how to get around in this environment. If you’re new to this or need a quick recap, it might be a good idea to check out that piece again to get a firm grip on the basics before diving in deeper.

Reinforcement Learning 101: Building a RL Agent

Today, we’re ready to take it up a bit. We will explore more complex aspects of RL, moving from simple setups to dynamic, ever-changing environments and more sophisticated ways for our agents to navigate through them. We’ll dive into the concept of the Markov Decision Process, which is very important for understanding how RL works at a deeper level. Plus, we’ll take a closer look at Q-learning, a key algorithm in RL that shows how agents can learn to make smart decisions in places like GridWorld, even when things are constantly changing.

Index
· 1: Beyond the Basics
∘ 1.1: Dynamic Environments

· 2: Markov Decision Process
∘ 2.1: Understanding MDP
∘ 2.2: The Math Behind MDP
∘ 2.3: The Math Behind Bellman Equations

· 3: Deep Dive into Q-Learning
∘ 3.1: Fundamentals of Q-Learning
∘ 3.2: The Math Behind Q-Learning

· 4: Q-Learning From Scratch
∘ 4.1: The GridWorld Environment
∘ 4.2: The Q-Learning Class

· 5: Next Steps and Future Directions
∘ 5.1: Current Problems and Limitations
∘ 5.2: Next Steps

· 6: Conclusion

1: Beyond the Basics

1.1: Dynamic Environments

When we first started exploring reinforcement learning (RL), we looked at simple, unchanging worlds. But as we move to dynamic environments, things get a lot more interesting. Unlike static setups where everything stays the same, dynamic environments are all about change. Obstacles move, goals shift, and rewards vary, making these settings much closer to the real world’s unpredictability.

What Makes Dynamic Environments Special?
Dynamic environments are key for teaching agents to adapt because they mimic the constant changes we face daily. Here, agents need to do more than just find the quickest route to a goal; they have to adjust their strategies as obstacles move, goals relocate, and rewards increase or decrease. This continuous learning and adapting are what could lead to true artificial intelligence.

Moving back to the environment we created in the last article, GridWorld, a 5×5 board with obstacles inside it. In this article, we’ll add some complexity to it making the obstacles shuffle randomly.

The Impact of Dynamic Environments on RL Agents
Dynamic environments train RL agents to be more robust and intelligent. Agents learn to adjust their strategies on the fly, a skill critical for navigating the real world where change is the only constant.

Facing a constantly evolving set of challenges, agents must make more nuanced decisions, balancing the pursuit of immediate rewards against the potential for future gains. Moreover, agents trained in dynamic environments are better equipped to generalize their learning to new, unseen situations, a key indicator of intelligent behavior.

2: Markov Decision Process

2.1: Understanding MDP

Before we dive into Q-Learning, let’s introduce the Markov Decision Process, or MDP for short. Think of MDP as the ABC of reinforcement learning. It offers a neat framework for understanding how an agent decides and learns from its surroundings. Picture MDP like a board game. Each square is a possible situation (state) the agent could find itself in, the moves it can make (actions), and the points it racks up after each move (rewards). The main aim is to collect as many points as possible.

Differing from the classic RL framework we introduced in the previous article, which focused on the concepts of states, actions, and rewards in a broad sense, MDP adds structure to these concepts by introducing transition probabilities and the optimization of policies. While the classic framework sets the stage for understanding reinforcement learning, MDP dives deeper, offering a mathematical foundation that accounts for the probabilities of moving from one state to another and optimizing the decision-making process over time. This detailed approach helps bridge the gap between theoretical learning and practical application, especially in environments where outcomes are partly uncertain and partly under the agent’s control.

Transition Probabilities
Ideally, we’d know exactly what happens next after an action. But life, much like MDP, is full of uncertainties. Transition probabilities are the rules that predict what comes next. If our game character jumps, will they land safely or fall? If the thermostat is cranked up, will the room get to the desired temperature?

Now imagine a maze game, where the agent aims to find the exit. Here, states are its spots in the maze, actions are which way it moves, and rewards come from exiting the maze with fewer moves.

MDP frames this scenario in a way that helps an RL agent figure out the best moves in different states to max out rewards. By playing this “game” repeatedly, the agent learns which actions work best in each state to score the highest, despite the uncertainties.

2.2: The Math Behind MDP

To get what the Markov Decision Process is about in reinforcement learning, it’s key to dive into its math. MDP gives us a solid setup for figuring out how to make decisions when things aren’t totally predictable and there’s some room for choice. Let’s break down the main math bits and pieces that paint the full picture of MDP.

Core Components of MDP
MDP is characterized by a tuple (S, A, P, R, γ), where:

• S is a set of states,
• A is a set of actions,
• P is the state transition probability matrix,
• R is the reward function, and
• γ is the discount factor.

While we covered the math behind states, actions, and the discount factor in the previous article, now we’ll introduce the math behind the state transition probability, and the reward function.

State Transition Probabilities
The state transition probability P(s′ ∣ s, a) defines the probability of transitioning from state s to state s′ after taking action a. This is a core element of the MDP that captures the dynamics of the environment. Mathematically, it’s expressed as:

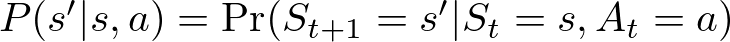
Here:

• s: The current state of the agent before taking the action.
• a: The action taken by the agent in state s.
• s′: The subsequent state the agent finds itself in after action a is taken.
• P(s′ ∣ s, a): The probability that action a in state s will lead to state s′.
• Pr⁡ denotes the probability, St​ represents the state at time t.
• St+1​ is the state at time t+1 after the action At​ is taken at time t.

This formula captures the essence of the stochastic nature of the environment. It acknowledges that the same action taken in the same state might not always lead to the same outcome due to the inherent uncertainties in the environment.

Consider a simple grid world where an agent can move up, down, left, or right. If the agent tries to move right, there might be a 90% chance it successfully moves right (s′=right), a 5% chance it slips and moves up instead (s′=up), and a 5% chance it slips and moves down (s′=down). There’s no probability of moving left since it’s the opposite direction of the intended action. Hence, for the action a=right from state s, the state transition probabilities might look like this:

• P(right ∣ s, right) = 0.9
• P(up ∣ s, right) = 0.05
• P(down ∣ s, right) = 0.05
• P(left ∣ s, right) = 0

Understanding and calculating these probabilities are fundamental for the agent to make informed decisions. By anticipating the likelihood of each possible outcome, the agent can evaluate the potential rewards and risks associated with different actions, guiding it towards decisions that maximize expected returns over time.

In practice, while exact state transition probabilities might not always be known or directly computable, various RL algorithms strive to estimate or learn these dynamics to achieve optimal decision-making. This learning process lies at the core of an agent’s ability to navigate and interact with complex environments effectively.

Reward Function
The reward function R(s, a, s′) specifies the immediate reward received after transitioning from state s to state s′ as a result of taking action a. It can be defined in various ways, but a common form is:

Here:

• Rt+1​: This is the reward received at the next time step after taking the action, which could vary depending on the stochastic elements of the environment.
• St​=s: This indicates the current state at time t.
• At​=a: This is the action taken by the agent in state s at time t.
• St+1​=s′: This denotes the state at the next time step t+1 after the action a has been taken.
• E[Rt+1​ ∣ St​=s, At​=a, St+1​=s′]: This represents the expected reward after taking action a in state s and ending up in state s′. The expectation E is taken over all possible outcomes that could result from the action, considering the probabilistic nature of the environment.

In essence, this function calculates the average or expected reward that the agent anticipates receiving for making a particular move. It takes into account the uncertain nature of the environment, as the same action in the same state may not always lead to the same next state or reward because of the probabilistic state transitions.

For example, if an agent is in a state representing its position in a grid, and it takes an action to move to another position, the reward function will calculate the expected reward of that move. If moving to that new position means reaching a goal, the reward might be high. If it means hitting an obstacle, the reward might be low or even negative. The reward function encapsulates the goals and rules of the environment, incentivizing the agent to take actions that will maximize its cumulative reward over time.

Policies
A policy π is a strategy that the agent follows, where π(a ∣ s) defines the probability of taking action a in state s. A policy can be deterministic, where the action is explicitly defined for each state, or stochastic, where actions are chosen according to a probability distribution:

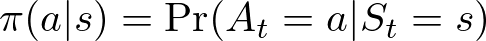
• π(a∣s): The probability that the agent takes action a given it is in state s.
• Pr(At​=a∣St​=s): The conditional probability that action a is taken at time t given the current state at time t is s.

Let’s consider a simple example of an autonomous taxi navigating in a city. Here the states are the different intersections within a city grid, and the actions are the possible maneuvers at each intersection, like ‘turn left’, ‘go straight’, ‘turn right’, or ‘pick up a passenger’.

The policy π might dictate that at a certain intersection (state), the taxi has the following probabilities for each action:

• π(’turn left’∣intersection) = 0.1
• π(’go straight’∣intersection) = 0.7
• π(’turn right’∣intersection) = 0.1
• π(’pick up passenger’∣intersection) = 0.1

In this example, the policy is stochastic because there are probabilities associated with each action rather than a single certain outcome. The taxi is most likely to go straight but has a small chance of taking other actions, which may be due to traffic conditions, passenger requests, or other variables.

The policy function guides the agent in selecting actions that it believes will maximize the expected return or reward over time, based on its current knowledge or strategy. Over time, as the agent learns, the policy may be updated to reflect new strategies that yield better results, making the agent’s behavior more sophisticated and better at achieving its goals.

Value Functions
Once I have my set of states, actions, and policies defined, we could ask ourselves the following question

What rewards can I expect in the long run if I start here and follow my game plan?

The answer is in the value function Vπ(s), which gives the expected return when starting in state s and following policy π thereafter:

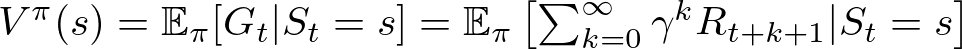
Where:

• Vπ(s): The value of state s under policy π.
• Gt​: The total discounted return from time t onwards.
• Eπ​[Gt​∣St​=s]: The expected return starting from state s following policy π.
• γ: The discount factor between 0 and 1, which determines the present value of future rewards — a way of expressing that immediate rewards are more certain than distant rewards.
• Rt+k+1​: The reward received at time t+k+1, which is k steps in the future.
• ∑k=0∞​: The sum of the discounted rewards from time t onward.

Imagine a game where you have a grid with different squares, and each square is a state that has different points (rewards). You have a policy π that tells you the probability of moving to other squares from your current square. Your goal is to collect as many points as possible.

For a particular square (state s), the value function Vπ(s) would be the expected total points you could collect from that square, discounted by how far in the future you receive them, following your policy π for moving around the grid. If your policy is to always move to the square with the highest immediate points, then Vπ(s) would reflect the sum of points you expect to collect, starting from s and moving to other squares according to π, with the understanding that points available further in the future are worth slightly less than points available right now (due to the discount factor γ).

In this way, the value function helps to quantify the long-term desirability of states given a particular policy, and it plays a key role in the agent’s learning process to improve its policy.

Action-Value Function
This function goes a step further, estimating the expected return of taking a specific action in a specific state and then following the policy. It’s like saying:

If I make this move now and stick to my strategy, what rewards am I likely to see?

While the value function V(s) is concerned with the value of states under a policy without specifying an initial action. In contrast, the action-value function Q(s, a) extends this concept to evaluate the value of taking a particular action in a state, before continuing with the policy.

The action-value function Qπ(s, a) represents the expected return of taking action a in state s and following policy π thereafter:

• Qπ(s, a): The value of taking action a in state s under policy π.
• Gt​: The total discounted return from time t onward.
• Eπ​[Gt ​∣ St​=s, At​=a]: The expected return after taking action a in state s the following policy π.
• γ: The discount factor, which determines the present value of future rewards.
• Rt+k+1​: The reward received k time steps in the future, after action a is taken at time t.
• ∑k=0∞​: The sum of the discounted rewards from time t onward.

The action-value function tells us what the expected return is if we start in state s, take action a, and then follow policy π after that. It takes into account not only the immediate reward received for taking action a but also all the future rewards that follow from that point on, discounted back to the present time.

Let’s say we have a robot vacuum cleaner with a simple task: clean a room and return to its charging dock. The states in this scenario could represent the vacuum’s location within the room, and the actions might include ‘move forward’, ‘turn left’, ‘turn right’, or ‘return to dock’.

The action-value function Qπ(s, a) helps the vacuum determine the value of each action in each part of the room. For instance:

• Qπ(middle of the room, ’move forward’) would represent the expected total reward the vacuum would get if it moves forward from the middle of the room and continues cleaning following its policy π.
• Qπ(near the dock, ’return to dock’) would represent the expected total reward for heading back to the charging dock to recharge.

The action-value function will guide the vacuum to make decisions that maximize its total expected rewards, such as cleaning as much as possible before needing to recharge.

In reinforcement learning, the action-value function is central to many algorithms, as it helps to evaluate the potential of different actions and informs the agent on how to update its policy to improve its performance over time.

2.3: The Math Behind Bellman Equations

In the world of Markov Decision Processes, the Bellman equations are fundamental. They act like a map, helping us navigate through the complex territory of decision-making to find the best strategies or policies. The beauty of these equations is how they simplify big challenges — like figuring out the best move in a game — into more manageable pieces.

They lay down the groundwork for what an optimal policy looks like — the strategy that maximizes rewards over time. They’re especially crucial in algorithms like Q-learning, where the agent learns the best actions through trial and error, adapting even when faced with unexpected situations.

Bellman Equation for Vπ(s)
This equation computes the expected return (total future rewards) of being in state s under a policy π. It sums up all the rewards an agent can expect to receive, starting from state s, and taking into account the likelihood of each subsequent state-action pair under the policy π. Essentially, it answers, “If I follow this policy, how good is it to be in this state?”

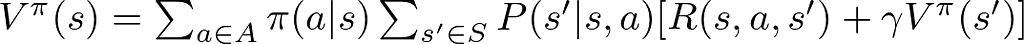
• π(a∣s) is the probability of taking action a in state s under policy π.
• P(s′ ∣ s, a) is the probability of transitioning to state s′ from state s after taking action a.
• R(s, a, s′) is the reward received after transitioning from s to s′ due to action a.
• γ is the discount factor, which values future rewards less than immediate rewards (0 ≤ γ < 1).
• Vπ​(s′) is the value of the subsequent state s′.

This equation calculates the expected value of a state s by considering all possible actions a, the likelihood of transitioning to a new state s′, the immediate reward R(s, a, s′), plus the discounted value of the subsequent state s′. It encapsulates the essence of planning under uncertainty, emphasizing the trade-offs between immediate rewards and future gains.

Bellman Equation for Qπ(s,a)
This equation goes a step further by evaluating the expected return of taking a specific action a in state s, and then following policy π afterward. It provides a detailed look at the outcomes of specific actions, giving insights like, “If I take this action in this state and then stick to my policy, what rewards can I expect?”

• P(s′ ∣ s, a) and R(s, a, s′) are as defined above.
• γ is the discount factor.
• π(a′ ∣ s′) is the probability of taking action a′ in the next state s′ under policy π.
• Qπ​(s′, a′) is the value of taking action a′ in the subsequent state s′.

This equation extends the concept of the state-value function by evaluating the expected utility of taking a specific action a in a specific state s. It accounts for the immediate reward and the discounted future rewards obtained by following policy π from the next state s′ onwards.

Both equations highlight the relationship between the value of a state (or a state-action pair) and the values of subsequent states, providing a way to evaluate and improve policies.

While value functions V(s) and action-value functions Q(s, a) represent the core objectives of learning in reinforcement learning — estimating the value of states and actions — the Bellman equations provide the recursive framework necessary for computing these values and enabling the agent to improve its decision-making over time.

3: Deep Dive into Q-Learning

Now that we’ve established all the foundational knowledge necessary for Q-Learning, let’s dive into action!

3.1: Fundamentals of Q-Learning

Q-learning works through trial and error. In particular, the agent checks out its surroundings, sometimes randomly picking paths to discover new ways to go. After it makes a move, the agent sees what happens and what kind of reward it gets. A good move, like getting closer to the goal, earns a positive reward. A not-so-good move, like smacking into a wall, means a negative reward. Based on what it learns, the agent updates its guide, bumping up the scores for good moves and lowering them for the bad ones. As the agent keeps exploring and updating its guide, it gets sharper at picking the best moves.

Let’s use the prior robot vacuum example. A Q-learning powered robot vacuum may firstly move around randomly. But as it keeps at it, it learns from the outcomes of its moves.

For instance, if moving forward means it cleans up a lot of dust (earning a high reward), the robot notes that going forward in that spot is a great move. If turning right causes it to bump into a chair (getting a negative reward), it learns that turning right there isn’t the best option.

The “cheat sheet” the robot builds is what Q-learning is all about. It’s a bunch of values (known as Q-values) that help guide the robot’s decisions. The higher the Q-value for a particular action in a specific situation, the better that action is. Over many cleaning rounds, the robot keeps refining its Q-values with every move it makes, constantly improving its cheat sheet until it nails down the best way to clean the room and zip back to its charger.

3.2: The Math Behind Q-Learning

Q-learning is a model-free reinforcement learning algorithm that seeks to find the best action to take given the current state. It’s about learning a function that will give us the best action to maximize the total future reward.

The Q-learning Update Rule: A Mathematical Formula
The mathematical heart of Q-learning lies in its update rule, which iteratively improves the Q-values that estimate the returns of taking certain actions from particular states. Here is the Q-learning update rule expressed in mathematical terms:

Let’s break down the components of this formula:

• Q(s, a): The current Q-value for a given state s and action a.
• α: The learning rate, a factor that determines how much new information overrides old information. It is a number between 0 and 1.
• R(s, a): The immediate reward received after taking action a in state s.
• γ: The discount factor, also a number between 0 and 1, which discounts the value of future rewards compared to immediate rewards.
• maxa′​Q(s′, a′): The maximum predicted reward for the next state s′, achieved by any action a′. This is the agent’s best guess at how valuable the next state will be.
• Q(s, a): The old Q-value before the update.

The essence of this rule is to adjust the Q-value for the state-action pair towards the sum of the immediate reward and the discounted maximum reward for the next state. The agent does this after every action it takes, slowly honing its Q-values towards the true values that reflect the best possible decisions.

The Q-values are initialized arbitrarily, and then the agent interacts with its environment, making observations, and updating its Q-values according to the rule above. Over time, with enough exploration of the state-action space, the Q-values converge to the optimal values, which reflect the maximum expected return one can achieve from each state-action pair.

This convergence means that the Q-values eventually provide the agent with a strategy for choosing actions that maximize the total expected reward for any given state. The Q-values essentially become a guide for the agent to follow, informing it of the value or quality of taking each action when in each state, hence the name “Q-learning”.

Difference with Bellman Equation
Comparing the Bellman Equation for Qπ(s, a) with the Q-learning update rule, we see that Q-learning essentially applies the Bellman equation in a practical, iterative manner. The key differences are:

• Learning from Experience: Q-learning uses the observed immediate reward R(s, a) and the estimated value of the next state maxa′​Q(s′, a′) directly from experience, rather than relying on the complete model of the environment (i.e., the transition probabilities P(s′ ∣ s, a)).
• Temporal Difference Learning: Q-learning’s update rule reflects a temporal difference learning approach, where the Q-values are updated based on the difference (error) between the estimated future rewards and the current Q-value.

4: Q-Learning From Scratch

To better understand every step of Q-Learning beyond its math, let’s build it from scratch. Take a look first at the whole code we will be using to create a reinforcement learning setup using a grid world environment and a Q-learning agent. The agent learns to navigate through the grid, avoiding obstacles and aiming for a goal.

Don’t worry if the code doesn’t seem clear, as we will break it down and go through it in detail later.

The code below is also accessible through this GitHub repo:

Reinforcement-Learning/Turtorial 2 – Q-Learning/main.py at main · cristianleoo/Reinforcement-Learning

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import pickle
import os

# GridWorld Environment
class GridWorld:
    """GridWorld environment with obstacles and a goal.
    The agent starts at the top-left corner and has to reach the bottom-right corner.
    The agent receives a reward of -1 at each step, a reward of -0.01 at each step in an obstacle, and a reward of 1 at the goal.
    
    Args:
        size (int): The size of the grid.
        num_obstacles (int): The number of obstacles in the grid.
        
    Attributes:
        size (int): The size of the grid.
        num_obstacles (int): The number of obstacles in the grid.
        obstacles (list): The list of obstacles in the grid.
        state_space (numpy.ndarray): The state space of the grid.
        state (tuple): The current state of the agent.
        goal (tuple): The goal state of the agent.
    
    Methods:
        generate_obstacles: Generate the obstacles in the grid.
        step: Take a step in the environment.
        reset: Reset the environment.
    """
    def __init__(self, size=5, num_obstacles=5):
        self.size = size
        self.num_obstacles = num_obstacles
        self.obstacles = []
        self.generate_obstacles()
        self.state_space = np.zeros((self.size, self.size))
        self.state = (0, 0)
        self.goal = (self.size-1, self.size-1)

    def generate_obstacles(self):
        """
        Generate the obstacles in the grid.
        The obstacles are generated randomly in the grid, except in the top-left and bottom-right corners.
        
        Args:
            None
        
        Returns:
            None
        """
        for _ in range(self.num_obstacles):
            while True:
                obstacle = (np.random.randint(self.size), np.random.randint(self.size))
                if obstacle not in self.obstacles and obstacle != (0, 0) and obstacle != (self.size-1, self.size-1):
                    self.obstacles.append(obstacle)
                    break

    def step(self, action):
        """
        Take a step in the environment.
        The agent takes a step in the environment based on the action it chooses.

        Args:
            action (int): The action the agent takes.
                0: up
                1: right
                2: down
                3: left
        
        Returns:
            state (tuple): The new state of the agent.
            reward (float): The reward the agent receives.
            done (bool): Whether the episode is done or not.
        """
        x, y = self.state
        if action == 0:  # up
            x = max(0, x-1)
        elif action == 1:  # right
            y = min(self.size-1, y+1)
        elif action == 2:  # down
            x = min(self.size-1, x+1)
        elif action == 3:  # left
            y = max(0, y-1)
        self.state = (x, y)
        if self.state in self.obstacles:
            return self.state, -1, True
        if self.state == self.goal:
            return self.state, 1, True
        return self.state, -0.01, False

    def reset(self):
        """
        Reset the environment.
        The agent is placed back at the top-left corner of the grid.

        Args:
            None
        
        Returns:
            state (tuple): The new state of the agent.
        """
        self.state = (0, 0)
        return self.state

# Q-Learning
class QLearning:
    """
    Q-Learning agent for the GridWorld environment.

    Args:
        env (GridWorld): The GridWorld environment.
        alpha (float): The learning rate.
        gamma (float): The discount factor.
        epsilon (float): The exploration rate.
        episodes (int): The number of episodes to train the agent.
    
    Attributes:
        env (GridWorld): The GridWorld environment.
        alpha (float): The learning rate.
        gamma (float): The discount factor.
        epsilon (float): The exploration rate.
        episodes (int): The number of episodes to train the agent.
        q_table (numpy.ndarray): The Q-table for the agent.
    
    Methods:
        choose_action: Choose an action for the agent to take.
        update_q_table: Update the Q-table based on the agent's experience.
        train: Train the agent in the environment.
        save_q_table: Save the Q-table to a file.
        load_q_table: Load the Q-table from a file.
    """
    def __init__(self, env, alpha=0.5, gamma=0.95, epsilon=0.1, episodes=10):
        self.env = env
        self.alpha = alpha
        self.gamma = gamma
        self.epsilon = epsilon
        self.episodes = episodes
        self.q_table = np.zeros((self.env.size, self.env.size, 4))

    def choose_action(self, state):
        """
        Choose an action for the agent to take.
        The agent chooses an action based on the epsilon-greedy policy.
        
        Args:
            state (tuple): The current state of the agent.
        
        Returns:
            action (int): The action the agent takes.
                0: up
                1: right
                2: down
                3: left
        """
        if np.random.uniform(0, 1) < self.epsilon:
            return np.random.choice([0, 1, 2, 3])  # exploration
        else:
            return np.argmax(self.q_table[state])  # exploitation

    def update_q_table(self, state, action, reward, new_state):
        """
        Update the Q-table based on the agent's experience.
        The Q-table is updated based on the Q-learning update rule.

        Args:
            state (tuple): The current state of the agent.
            action (int): The action the agent takes.
            reward (float): The reward the agent receives.
            new_state (tuple): The new state of the agent.

        Returns:
            None
        """
        self.q_table[state][action] = (1 - self.alpha) * self.q_table[state][action] + 
            self.alpha * (reward + self.gamma * np.max(self.q_table[new_state]))

    def train(self):
        """
        Train the agent in the environment.
        The agent is trained in the environment for a number of episodes.
        The agent's experience is stored and returned.

        Args:
            None
        
        Returns:
            rewards (list): The rewards the agent receives at each step.
            states (list): The states the agent visits at each step.
            starts (list): The start of each new episode.
            steps_per_episode (list): The number of steps the agent takes in each episode.
        """
        rewards = []
        states = []  # Store states at each step
        starts = []  # Store the start of each new episode
        steps_per_episode = []  # Store the number of steps per episode
        steps = 0  # Initialize the step counter outside the episode loop
        episode = 0
        while episode < self.episodes:
            state = self.env.reset()
            total_reward = 0
            done = False
            while not done:
                action = self.choose_action(state)
                new_state, reward, done = self.env.step(action)
                self.update_q_table(state, action, reward, new_state)
                state = new_state
                total_reward += reward
                states.append(state)  # Store state
                steps += 1  # Increment the step counter
                if done and state == self.env.goal:  # Check if the agent has reached the goal
                    starts.append(len(states))  # Store the start of the new episode
                    rewards.append(total_reward)
                    steps_per_episode.append(steps)  # Store the number of steps for this episode
                    steps = 0  # Reset the step counter
                    episode += 1
        return rewards, states, starts, steps_per_episode
    
    def save_q_table(self, filename):
        """
        Save the Q-table to a file.
        
        Args:
            filename (str): The name of the file to save the Q-table to.
            
        Returns:
            None
        """
        filename = os.path.join(os.path.dirname(__file__), filename)
        with open(filename, 'wb') as f:
            pickle.dump(self.q_table, f)

    def load_q_table(self, filename):
        """
        Load the Q-table from a file.

        Args:
            filename (str): The name of the file to load the Q-table from.
        
        Returns:
            None
        """
        filename = os.path.join(os.path.dirname(__file__), filename)
        with open(filename, 'rb') as f:
            self.q_table = pickle.load(f)


# Initialize environment and agent
for i in range(10):
    env = GridWorld(size=5, num_obstacles=5)
    agent = QLearning(env)

    # Load the Q-table if it exists
    if os.path.exists(os.path.join(os.path.dirname(__file__), 'q_table.pkl')):
        agent.load_q_table('q_table.pkl')

    # Train the agent and get rewards
    rewards, states, starts, steps_per_episode = agent.train()  # Get starts and steps_per_episode as well

    # Save the Q-table
    agent.save_q_table('q_table.pkl')

    # Visualize the agent moving in the grid
    fig, ax = plt.subplots()

    def update(i):
        """
        Update the grid with the agent's movement.
        
        Args:
            i (int): The current step.
        
        Returns:
            None
        """
        ax.clear()
        # Calculate the cumulative reward up to the current step
        cumulative_reward = sum(rewards[:i+1])
        # Find the current episode
        current_episode = next((j for j, start in enumerate(starts) if start > i), len(starts)) - 1
        # Calculate the number of steps since the start of the current episode
        if current_episode < 0:
            steps = i + 1
        else:
            steps = i - starts[current_episode] + 1
        ax.set_title(f"Iteration: {current_episode+1}, Total Reward: {cumulative_reward:.2f}, Steps: {steps}")
        grid = np.zeros((env.size, env.size))
        for obstacle in env.obstacles:
            grid[obstacle] = -1
        grid[env.goal] = 1
        grid[states[i]] = 0.5  # Use states[i] instead of env.state
        ax.imshow(grid, cmap='cool')

    ani = animation.FuncAnimation(fig, update, frames=range(len(states)), repeat=False)

    # After the animation
    print(f"Environment number {i+1}")
    for i, steps in enumerate(steps_per_episode, 1):
        print(f"Iteration {i}: {steps} steps")
    print(f"Total reward: {sum(rewards):.2f}")
    print()

    plt.show()

That was a lot of code! Let’s break down this code into smaller, more understandable steps. Here’s what each part does:

4.1: The GridWorld Environment

This class represents a grid environment where an agent can move around, avoid obstacles, and reach a goal.

Initialization (__init__ method)

def __init__(self, size=5, num_obstacles=5):
    self.size = size
    self.num_obstacles = num_obstacles
    self.obstacles = []
    self.generate_obstacles()
    self.state_space = np.zeros((self.size, self.size))
    self.state = (0, 0)
    self.goal = (self.size-1, self.size-1)

When you create a new GridWorld, you specify the size of the grid and the number of obstacles. The grid is square, so size=5 means a 5×5 grid. The agent starts at the top-left corner (0, 0) and aims to reach the bottom-right corner (size-1, size-1). The obstacles are held in self.obstacles, which is an empty list of obstacles that will be filled with the locations of the obstacles. The generate_obstacles() method is then called to randomly place obstacles in the grid.

Therefore, we could expect an environment like the following:

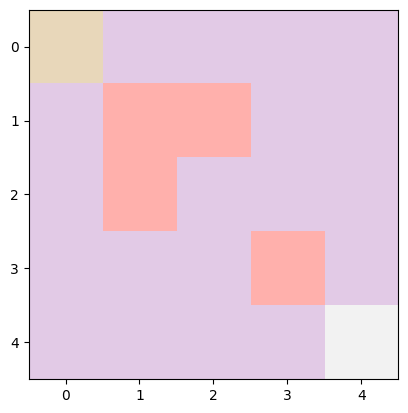
In the environment above the top-left block is the starting state, the bottom-right block is the goal, and the pink blocks in the middle are the obstacles. Note that the obstacles will vary everytime you create an environment, as they are generated randomly.

Generating Obstacles (generate_obstacles method)

def generate_obstacles(self):
    for _ in range(self.num_obstacles):
        while True:
            obstacle = (np.random.randint(self.size), np.random.randint(self.size))
            if obstacle not in self.obstacles and obstacle != (0, 0) and obstacle != (self.size-1, self.size-1):
                self.obstacles.append(obstacle)
                  break

This method places num_obstacles randomly within the grid. It ensures that obstacles don’t overlap with the starting point or the goal.

It does this by looping until the specified number of obstacles ( self.num_obstacles)have been placed. In every loop, it randomly selects a position in the grid, then if the position is not already an obstacle, and not the start or goal, it’s added to the list of obstacles.

Taking a Step (step method)

def step(self, action):
    x, y = self.state
    if action == 0:  # up
        x = max(0, x-1)
    elif action == 1:  # right
        y = min(self.size-1, y+1)
    elif action == 2:  # down
        x = min(self.size-1, x+1)
    elif action == 3:  # left
        y = max(0, y-1)
    self.state = (x, y)
    if self.state in self.obstacles:
        return self.state, -1, True
    if self.state == self.goal:
        return self.state, 1, True
    return self.state, -0.01, False

The step method moves the agent according to the action (0 for up, 1 for right, 2 for down, 3 for left) and updates its state. It also checks the new position to see if it’s an obstacle or a goal.

It does that by taking the current state (x, y), which is the current location of the agent. Then, it changes x or y based on the action (0 for up, 1 for right, 2 for down, 3 for left), ensuring the agent doesn’t move outside the grid boundaries. It updates self.state to this new position. Then it checks if the new state is an obstacle or the goal and returns the corresponding reward and whether the episode is finished (done).

Resetting the Environment (reset method)

def reset(self):
    self.state = (0, 0)
    return self.state

This function puts the agent back at the starting point. It’s used at the beginning of a new learning episode.

It simply sets self.state back to (0, 0) and returns this as the new state.

4.2: The Q-Learning Class

This is a Python class that represents a Q-learning agent, which will learn how to navigate the GridWorld.

Initialization (__init__ method)

def __init__(self, env, alpha=0.5, gamma=0.95, epsilon=0.1, episodes=10):
    self.env = env
    self.alpha = alpha
    self.gamma = gamma
    self.epsilon = epsilon
    self.episodes = episodes
    self.q_table = np.zeros((self.env.size, self.env.size, 4))

When you create a QLearning agent, you provide it with the environment to learn from self.env, which is the GridWorld environment in our case; a learning rate alpha, which controls how new information affects the existing Q-values; a discount factor gamma, which determines the importance of future rewards; an exploration rate epsilon, which controls the trade-off between exploration and exploitation.

Then, we also initialize the number of episodes for training. The Q-table, which stores the agent’s knowledge, and it’s a 3D numpy array of zeros with dimensions (env.size, env.size, 4), representing the Q-values for each state-action pair. 4 is the number of possible actions the agent can take in every state.

Choosing an Action (choose_action method)

def choose_action(self, state):
    if np.random.uniform(0, 1) < self.epsilon:
        return np.random.choice([0, 1, 2, 3])  # exploration
    else:
        return np.argmax(self.q_table[state])  # exploitation

The agent picks an action based on the epsilon-greedy policy. Most of the time, it chooses the best-known action (exploitation), but sometimes it randomly explores other actions.

Here, epsilon is the probability a random action is chosen. Otherwise, the action with the highest Q-value for the current state is chosen (argmax over the Q-values).

In our example, we set epsilon it to 0.1, which means that the agent will take a random action 10% of the time. Therefore, when np.random.uniform(0,1) generating a number lower than 0.1, a random action will be taken. This is done to prevent the agent from being stuck on a suboptimal strategy, and instead going out and exploring before being set on one.

Updating the Q-Table (update_q_table method)

def update_q_table(self, state, action, reward, new_state):
    self.q_table[state][action] = (1 - self.alpha) * self.q_table[state][action] + 
        self.alpha * (reward + self.gamma * np.max(self.q_table[new_state]))

After the agent takes an action, it updates its Q-table with the new knowledge. It adjusts the value of the action based on the immediate reward and the discounted future rewards from the new state.

It updates the Q-table using the Q-learning update rule. It modifies the value for the state-action pair in the Q-table (self.q_table[state][action]) based on the received reward and the estimated future rewards (using np.max(self.q_table[new_state]) for the future state).

Training the Agent (train method)

def train(self):
    rewards = []
    states = []  # Store states at each step
    starts = []  # Store the start of each new episode
    steps_per_episode = []  # Store the number of steps per episode
    steps = 0  # Initialize the step counter outside the episode loop
    episode = 0
    while episode < self.episodes:
        state = self.env.reset()
        total_reward = 0
        done = False
        while not done:
            action = self.choose_action(state)
            new_state, reward, done = self.env.step(action)
            self.update_q_table(state, action, reward, new_state)
            state = new_state
            total_reward += reward
            states.append(state)  # Store state
            steps += 1  # Increment the step counter
            if done and state == self.env.goal:  # Check if the agent has reached the goal
                starts.append(len(states))  # Store the start of the new episode
                rewards.append(total_reward)
                steps_per_episode.append(steps)  # Store the number of steps for this episode
                steps = 0  # Reset the step counter
                episode += 1
    return rewards, states, starts, steps_per_episode

This function is pretty straightforward, it runs the agent through many episodes using a while loop. In every episode, it first resets the environment by placing the agent in the starting state (0,0). Then, it chooses actions, updates the Q-table, and keeps track of the total rewards and steps it takes.

Saving and Loading the Q-Table (save_q_table and load_q_table methods)

def save_q_table(self, filename):
    filename = os.path.join(os.path.dirname(__file__), filename)
    with open(filename, 'wb') as f:
        pickle.dump(self.q_table, f)

def load_q_table(self, filename):
    filename = os.path.join(os.path.dirname(__file__), filename)
    with open(filename, 'rb') as f:
        self.q_table = pickle.load(f)

These methods are used to save the learned Q-table to a file and load it back. They use the pickle module to serialize (pickle.dump) and deserialize (pickle.load) the Q-table, allowing the agent to resume learning without starting from scratch.

Running the Simulation

Finally, the script initializes the environment and the agent, optionally loads an existing Q-table, and then starts the training process. After training, it saves the updated Q-table. There’s also a visualization section that shows the agent moving through the grid, which helps you see what the agent has learned.

Initialization

Firstly, the environment and agent are initialized:

env = GridWorld(size=5, num_obstacles=5)
agent = QLearning(env)

Here, a GridWorld of size 5×5 with 5 obstacles is created. Then, a QLearning agent is initialized using this environment.

Loading and Saving the Q-table
If there’s a Q-table file already saved (‘q_table.pkl’), it’s loaded, which allows the agent to continue learning from where it left off:

if os.path.exists(os.path.join(os.path.dirname(__file__), 'q_table.pkl')):
    agent.load_q_table('q_table.pkl')

After the agent is trained for the specified number of episodes, the updated Q-table is saved:

agent.save_q_table('q_table.pkl')

This ensures that the agent’s learning is not lost and can be used in future training sessions or actual navigation tasks.

Training the Agent
The agent is trained by calling the train method, which runs through the specified number of episodes, allowing the agent to explore the environment, update its Q-table, and track its progress:

rewards, states, starts, steps_per_episode = agent.train()

During training, the agent chooses actions, updates the Q-table, observes rewards, and keeps track of states visited. All of this information is used to adjust the agent’s policy (i.e., the Q-table) to improve its decision-making over time.

Visualization

After training, the code uses matplotlib to create an animation showing the agent’s journey through the grid. It visualizes how the agent moves, where the obstacles are, and the path to the goal:

fig, ax = plt.subplots()
def update(i):
    # Update the grid visualization based on the agent's current state
    ax.clear()
    # Calculate the cumulative reward up to the current step
    cumulative_reward = sum(rewards[:i+1])
    # Find the current episode
    current_episode = next((j for j, start in enumerate(starts) if start > i), len(starts)) - 1
    # Calculate the number of steps since the start of the current episode
    if current_episode < 0:
        steps = i + 1
    else:
        steps = i - starts[current_episode] + 1
    ax.set_title(f"Iteration: {current_episode+1}, Total Reward: {cumulative_reward:.2f}, Steps: {steps}")
    grid = np.zeros((env.size, env.size))
    for obstacle in env.obstacles:
        grid[obstacle] = -1
    grid[env.goal] = 1
    grid[states[i]] = 0.5  # Use states[i] instead of env.state
    ax.imshow(grid, cmap='cool')
ani = animation.FuncAnimation(fig, update, frames=range(len(states)), repeat=False)
plt.show()

This visualization is not only a nice way to see what the agent has learned, but it also provides insight into the agent’s behavior and decision-making process.

By running this simulation multiple times (as indicated by the loop for i in range(10):), the agent can have multiple learning sessions, which can potentially lead to improved performance as the Q-table gets refined with each iteration.

Now try this code out, and check how many steps it takes for the agent to reach the goal by iteration. Furthermore, try to increase the size of the environment, and see how this affects the performance.

5: Next Steps and Future Directions

As we take a step back to evaluate our journey with Q-learning and the GridWorld setup, it’s important to appreciate our progress but also to note where we hit snags. Sure, we’ve got our agents moving around a basic environment, but there are a bunch of hurdles we still need to jump over to kick their skills up a notch.

5.1: Current Problems and Limitations

Limited Complexity
Right now, GridWorld is pretty basic and doesn’t quite match up to the messy reality of the world around us, which is full of unpredictable twists and turns.

Scalability Issues
When we try to make the environment bigger or more complex, our Q-table (our cheat sheet of sorts) gets too bulky, making Q-learning slow and a tough nut to crack.

One-Size-Fits-All Rewards
We’re using a simple reward system — dodging obstacles losing points, and reaching the goal and gaining points. But we’re missing out on the nuances, like varying rewards for different actions that could steer the agent more subtly.

Discrete Actions and States
Our current Q-learning vibe works with clear-cut states and actions. But life’s not like that; it’s full of shades of grey, requiring more flexible approaches.

Lack of Generalization
Our agent learns specific moves for specific situations without getting the knack for winging it in scenarios it hasn’t seen before or applying what it knows to different but similar tasks.

5.2: Next Steps

Policy Gradient Methods
Policy gradient methods represent a class of algorithms in reinforcement learning that optimize the policy directly. They are particularly well-suited for problems with:

• High-dimensional or continuous action spaces.
• The need for fine-grained control over the actions.
• Complex environments where the agent must learn more abstract concepts.

The next article will cover everything necessary to understand and implement policy gradient methods.

We’ll start with the conceptual underpinnings of policy gradient methods, explaining how they differ from value-based approaches and their advantages.

We’ll dive into algorithms like REINFORCE and Actor-Critic methods, exploring how they work and when to use them. We’ll discuss the exploration strategies used in policy gradient methods, which are crucial for effective learning in complex environments.

A key challenge with policy gradients is high variance in the updates. We will look into techniques like baselines and advantage functions to tackle this issue.

A More Complex Environment
To truly harness the power of policy gradient methods, we will introduce a more complex environment. This environment will have a continuous state and action space, presenting a more realistic and challenging learning scenario. Multiple paths to success, require the agent to develop nuanced strategies. The possibility of more dynamic elements, such as moving obstacles or changing goals.

Stay tuned as we prepare to embark on this exciting journey into the world of policy gradient methods, where we’ll empower our agents to tackle challenges of increasing complexity and closer to real-world applications.

6: Conclusion

As we conclude this article, it’s clear that the journey through the fundamentals of reinforcement learning has set a robust stage for our next foray into the field. We’ve seen our agent start from scratch, learning to navigate the straightforward corridors of the GridWorld, and now it stands on the brink of stepping into a world that’s richer and more reflective of the complexities it must master.

It was a lot, but you made it to the end. Congrats! I hope you enjoyed this article. If so consider leaving a clap and following me, as I will regularly post similar articles. Let me know what you think about the article, what you would like to see more. Consider leaving a clap or two and follow me to stay updated.

Reinforcement Learning 101: Q-Learning was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.