Originally appeared here:
3 million smart toothbrushes were not used in a DDoS attack after all, but it could happen
Year: 2024
-
3 million smart toothbrushes were not used in a DDoS attack after all, but it could happen
[UPDATED] What’s next, malware-infected dental floss? But seriously: It’s a reminder that even the smallest smart home devices can be a threat. Here’s how to protect yourself. -
It’s exactly 40 years since NASA achieved this remarkable first in orbit
On February 7, 1984, NASA astronaut Bruce McCandless II achieved a remarkable feat when he performed the first untethered spacewalk.Go Here to Read this Fast! It’s exactly 40 years since NASA achieved this remarkable first in orbit
Originally appeared here:
It’s exactly 40 years since NASA achieved this remarkable first in orbit -
Bluesky has added almost a million users one day after opening to the public
Bluesky, the open source Twitter alternative, has seen a surge in new users just one day after opening its platform up to the public. The service has gained more than 850,000 users bringing its total sign-ups to just over 4 million.
The service had been in an invitation-only beta for about a year and had grown to just over 3 million users when it officially opened to the public. It currently has close to 4.1 million sign-ups, according to an online tracker. “Things are rolling over here,” Bluesky CEO Jay Graber wrote in a post on X.
The surge in new users suggests that there is still ample curiosity about the Jack Dorsey-backed platform that began as an internal project at Twitter in 2019. It also indicated that Meta hasn’t entirely cornered the market for a text-based Twitter alternative. The company’s Threads app has grown to 130 million monthly users, Meta announced last week.
Graber has said that Bluesky intended to grow at a slower pace so that it could build it the platform, and the underlying protocol, without the added pressure sudden surges in growth can cause. Some of those concerns were borne out over the last day as the spike in activity led to some technical issues on the site, including problems with the app’s custom feeds and a brief outage overnight. The outage was resolved within a couple hours, according to the company.
Much of Bluesky’s future success will hinge on whether it can maintain new growth and keep the interest of all its new users. Threads also saw an initial spike in new users, only for it to drop-off before eventually rebounding.
Though Bluesky may look a bit like Threads or X, it’s a fundamentally different kind of platform and part of the growing movement for decentralized social media. Its open-source protocol functions like a “permanently open” API, according to Graber, and the site already has dozens of developers building their own experiences. Bluesky also offers more customization features for users, with features like custom algorithms and the ability to choose your own content moderation settings.
This article originally appeared on Engadget at https://www.engadget.com/bluesky-has-added-almost-a-million-users-one-day-after-opening-to-the-public-004854186.html?src=rss
Originally appeared here:
Bluesky has added almost a million users one day after opening to the public -

Quordle today – hints and answers for Thursday, February 8 (game #745)
 Looking for Quordle clues? We can help. Plus get the answers to Quordle today and past solutions.
Looking for Quordle clues? We can help. Plus get the answers to Quordle today and past solutions.Go Here to Read this Fast! Quordle today – hints and answers for Thursday, February 8 (game #745)
Originally appeared here:
Quordle today – hints and answers for Thursday, February 8 (game #745) -

Today’s Wordle answer and hints for game #964, Thursday, February 8
 Looking for Wordle hints? We can help. Plus get the answers to Wordle today and yesterday.Today’s Wordle answer and hints for game #964, Thursday, February 8Today’s Wordle answer and hints for game #964, Thursday, February 8
Looking for Wordle hints? We can help. Plus get the answers to Wordle today and yesterday.Today’s Wordle answer and hints for game #964, Thursday, February 8Today’s Wordle answer and hints for game #964, Thursday, February 8 -
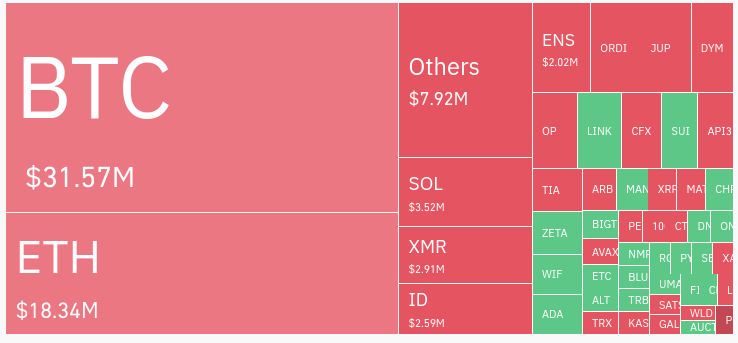
Bitcoin surpasses $44.2k, a level last seen days after Bitcoin ETF approvals
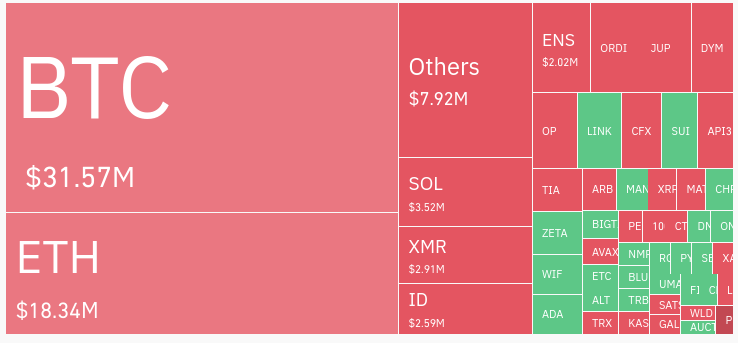
Bitcoin prices rose above $44,200 on Feb. 7, a price level observed shortly after spot Bitcoin ETFs gained approval last month. Specifically, Bitcoin (BTC) is up 2.5% over 24 hours as of 10:45 p.m. UTC, with a market price of $44,263.78 and a capitalization of $868 billion. This marks a nearly one-month high, as BTC […]
The post Bitcoin surpasses $44.2k, a level last seen days after Bitcoin ETF approvals appeared first on CryptoSlate.
Originally appeared here:
Bitcoin surpasses $44.2k, a level last seen days after Bitcoin ETF approvals -
Shiba Inu whales load up trillions in SHIB – To what end?
The supply held by non-exchange addresses outweighed those held by top exchange wallets.
If capital flow increases, SHIB might climb to $0.00002.Top non-exchange Shiba Inu [SHIB] addresses
The post Shiba Inu whales load up trillions in SHIB – To what end? appeared first on AMBCrypto.
Go here to Read this Fast! Shiba Inu whales load up trillions in SHIB – To what end?
Originally appeared here:
Shiba Inu whales load up trillions in SHIB – To what end? -

But What is Backpropagation, Really? (Part 1)

Implementing a simple neural network framework from scratch

Trees — the core of computation. Source: Adrian Infernus on Unsplash. Despite doing some work and research in the AI ecosystem for some time, I didn’t truly stop to think about backpropagation and gradient updates within neural networks until recently. This article seeks to rectify that and will hopefully provide a thorough yet easy-to-follow dive into the topic by implementing a simple (yet somewhat powerful) neural network framework from scratch.
Elementary Operations — The Network’s Core
Fundamentally, a neural network is just a mathematical function from our input space to our desired output space. In fact, we can effectively “unwrap” any neural network into a function. Consider, for instance, the following simple neural network with two layers and one input:
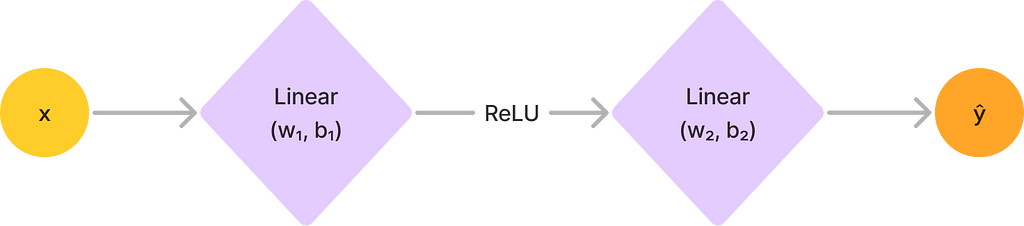
A simple neural net with two layers and a ReLU activation. Here, the linear networks have weights wₙ and biases bₙ We can now construct an equivalent function by going forwards layer by layer, starting from the input. Let’s follow our final function layer by layer:
- At the input, we start with the identity function pred(x) = x
- At the first linear layer, we get pred(x) = w₁x + b₁
- The ReLU nets us pred(x) = max(0, w₁x + b₁)
- At the final layer, we get pred(x) = w₂(max(0, w₁x + b₁)) + b₂
With more complicated nets, these functions of course get unwieldy, but the point is that we can construct such representations of neural networks.
We can go one step further though — functions of this form are not extremely convenient for computation, but we can parse them into a more useful form, namely a syntax tree. For our simple net, the tree would look like this:

A tree representation of our function In this tree form, our leaves are parameters, constants, and inputs, and the other nodes are elementary operations whose arguments are their children. Of course, these elementary operations don’t have to be binary — the sigmoid operation, for instance, is unary (and so is ReLU if we don’t represent it as a max of 0 and x), and we can choose to support multiplication and addition of more than one input.
By thinking of our network as a tree of these elementary operations, we can now do a lot of things very easily with recursion, which will form the basis of both our backpropagation and forward propagation algorithms. In code, we can define a recursive neural network class that looks like this:
from dataclasses import dataclass, field
from typing import List
@dataclass
class NeuralNetNode:
"""A node in our neural network tree"""
children: List['NeuralNetNode'] = field(default_factory=list)
def op(self, x: List[float]) -> float:
"""The operation that this node performs"""
raise NotImplementedError
def forward(self) -> float:
"""Evaluate this node on the given input"""
return self.op([child.forward() for child in self.children])
# This is just for convenience
def __call__(self) -> List[float]:
return self.forward()
def __repr__(self):
return f'{self.__class__.__name__}({self.children})'Going Backwards — Recursive Chain Rule
Suppose now that we have a differentiable loss function for our neural network, say MSE. Recall that MSE (for one sample) is defined as follows:
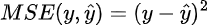
The MSE loss function We now wish to update our parameters (the green circles in our tree representation) given the value of our loss. To do this, we need the derivative of our loss function with respect to each parameter. Calculating this directly from the loss is extremely difficult though — after all, our MSE is calculated in terms of the value predicted by our neural net, which can be an extraordinarily complicated function.
This is where very useful piece of mathematics — the chain rule — comes into play. Instead of being forced to compute our highly complex derivatives from the get-go, we can instead compute a series of simpler derivatives.
It turns out that the chain rule meshes very well with our recursive tree structure. The idea basically works as follows: assuming that we have simple enough elementary operations, each elementary operation knows its derivative with respect to all of its arguments. Given the derivative from the parent operation, we can thus compute the derivative of each child operation with respect to the loss function through simple multiplication. For a simple linear regression model using MSE, we can diagram it as follows:

Forward and backward pass diagrams for a simple linear classifier with weight w1, bias b1. Note h₁ is just the variable returned by our multiplication operation, like our prediction is returned by addition. Of course, some of our nodes don’t do anything with their derivatives — namely, only our leaf nodes care. But now each node can get the derivative of its output with respect to the loss function through this recursive process. We can thus add the following methods to our NeuralNetNode class:
def grad(self) -> List[float]:
"""The gradient of this node with respect to its inputs"""
raise NotImplementedError
def backward(self, derivative_from_parent: float):
"""Propagate the derivative from the parent to the children"""
self.on_backward(derivative_from_parent)
deriv_wrt_children = self.grad()
for child, derivative_wrt_child in zip(self.children, deriv_wrt_children):
child.backward(derivative_from_parent * derivative_wrt_child)
def on_backward(self, derivative_from_parent: float):
"""Hook for subclasses to override. Things like updating parameters"""
passExercise 1: Try creating one of these trees for a simple linear regression model and perform the recursive gradient updates by hand for a couple of steps.
Note: For simplicity’s sake, we require our nodes to have only one parent (or none at all). If each node is allowed to have multiple parents, our backwards() algorithm becomes somewhat more complicated as each child needs to sum the derivative of its parents to compute its own. We can do this iteratively with a topological sort (e.g. see here) or still recursively, i.e. with reverse accumulation (though in this case we would need to do a second pass to actually update all of the parameters). This isn’t extraordinarily difficult, so I’ll leave it as an exercise to the reader (and will talk about it more in part 2, stay tuned).
Finishing Our Framework
Building Models
The rest of our code really just involves implementing parameters, inputs, and operations, and of course running our training. Parameters and inputs are fairly simple constructs:
import random
@dataclass
class Input(NeuralNetNode):
"""A leaf node that represents an input to the network"""
value: float=0.0
def op(self, x):
return self.value
def grad(self) -> List[float]:
return [1.0]
def __repr__(self):
return f'{self.__class__.__name__}({self.value})'
@dataclass
class Parameter(NeuralNetNode):
"""A leaf node that represents a parameter to the network"""
value: float=field(default_factory=lambda: random.uniform(-1, 1))
learning_rate: float=0.01
def op(self, x):
return self.value
def grad(self):
return [1.0]
def on_backward(self, derivative_from_parent: float):
self.value -= derivative_from_parent * self.learning_rate
def __repr__(self):
return f'{self.__class__.__name__}({self.value})'Operations are slightly more complicated, though not too much so — we just need to calculate their gradients properly. Below are implementations of some useful operations:
import math
@dataclass
class Operation(NeuralNetNode):
"""A node that performs an operation on its inputs"""
pass
@dataclass
class Add(Operation):
"""A node that adds its inputs"""
def op(self, x):
return sum(x)
def grad(self):
return [1.0] * len(self.children)
@dataclass
class Multiply(Operation):
"""A node that multiplies its inputs"""
def op(self, x):
return math.prod(x)
def grad(self):
grads = []
for i in range(len(self.children)):
cur_grad = 1
for j in range(len(self.children)):
if i == j:
continue
cur_grad *= self.children[j].forward()
grads.append(cur_grad)
return grads
@dataclass
class ReLU(Operation):
"""
A node that applies the ReLU function to its input.
Note that this should only have one child.
"""
def op(self, x):
return max(0, x[0])
def grad(self):
return [1.0 if self.children[0].forward() > 0 else 0.0]
@dataclass
class Sigmoid(Operation):
"""
A node that applies the sigmoid function to its input.
Note that this should only have one child.
"""
def op(self, x):
return 1 / (1 + math.exp(-x[0]))
def grad(self):
return [self.forward() * (1 - self.forward())]The operation superclass here is not useful yet, though we will need it to more easily find our model’s inputs later.
Notice how often the gradients of the functions require the values from their children, hence we require calling the child’s forward() method. We will touch upon this more in a little bit.
Defining a neural network in our framework is a bit verbose but is very similar to constructing a tree. Here, for instance, is code for a simple linear classifier in our framework:
linear_classifier = Add([
Multiply([
Parameter(),
Input()
]),
Parameter()
])Using Our Models
To run a prediction with our model, we have to first populate the inputs in our tree and then call forward() on the parent. To populate the inputs though, we first need to find them, hence we add the following method to our Operation class (we don’t add this to our NeuralNetNode class since the Input type isn’t defined there yet):
def find_input_nodes(self) -> List[Input]:
"""Find all of the input nodes in the subtree rooted at this node"""
input_nodes = []
for child in self.children:
if isinstance(child, Input):
input_nodes.append(child)
elif isinstance(child, Operation):
input_nodes.extend(child.find_input_nodes())
return input_nodesWe can now add the predict() method to the Operation class:
def predict(self, inputs: List[float]) -> float:
"""Evaluate the network on the given inputs"""
input_nodes = self.find_input_nodes()
assert len(input_nodes) == len(inputs)
for input_node, value in zip(input_nodes, inputs):
input_node.value = value
return self.forward()Exercise 2: The current way we implemented predict() is somewhat inefficient since we need to traverse the tree to find all the inputs every time we run predict(). Write a compile() method that caches the operation’s inputs when it is run.
Training our models is now very straightforward:
from typing import Callable, Tuple
def train_model(
model: Operation,
loss_fn: Callable[[float, float], float],
loss_grad_fn: Callable[[float, float], float],
data: List[Tuple[List[float], float]],
epochs: int=1000,
print_every: int=100
):
"""Train the given model on the given data"""
for epoch in range(epochs):
total_loss = 0.0
for x, y in data:
prediction = model.predict(x)
total_loss += loss_fn(y, prediction)
model.backward(loss_grad_fn(y, prediction))
if epoch % print_every == 0:
print(f'Epoch {epoch}: loss={total_loss/len(data)}')Here, for instance, is how we would train a linear Fahrenheit to Celsius classifier using our framework:
def mse_loss(y_true: float, y_pred: float) -> float:
return (y_true - y_pred) ** 2
def mse_loss_grad(y_true: float, y_pred: float) -> float:
return -2 * (y_true - y_pred)
def fahrenheit_to_celsius(x: float) -> float:
return (x - 32) * 5 / 9
def generate_f_to_c_data() -> List[List[float]]:
data = []
for _ in range(1000):
f = random.uniform(-1, 1)
data.append([[f], fahrenheit_to_celsius(f)])
return data
linear_classifier = Add([
Multiply([
Parameter(),
Input()
]),
Parameter()
])
train_model(linear_classifier, mse_loss, mse_loss_grad, generate_f_to_c_data())After running this, we get
print(linear_classifier)
print(linear_classifier.predict([32]))
>> Add(children=[Multiply(children=[Parameter(0.5555555555555556), Input(0.8930639016107234)]), Parameter(-17.777777777777782)])
>> -1.7763568394002505e-14Which correctly corresponds to a linear classifier with weight 0.56, bias -17.78 (which is the Fahrenheit to Celsius formula)
We can, of course, also train much more complex models, e.g. here is one for predicting if a point (x, y) is above or below the line y = x:
def bce_loss(y_true: float, y_pred: float, eps: float=0.00000001) -> float:
y_pred = min(max(y_pred, eps), 1 - eps)
return -y_true * math.log(y_pred) - (1 - y_true) * math.log(1 - y_pred)
def bce_loss_grad(y_true: float, y_pred: float, eps: float=0.00000001) -> float:
y_pred = min(max(y_pred, eps), 1 - eps)
return (y_pred - y_true) / (y_pred * (1 - y_pred))
def generate_binary_data():
data = []
for _ in range(1000):
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
data.append([(x, y), 1 if y > x else 0])
return data
model_binary = Sigmoid(
[
Add(
[
Multiply(
[
Parameter(),
ReLU(
[
Add(
[
Multiply(
[
Parameter(),
Input()
]
),
Multiply(
[
Parameter(),
Input()
]
),
Parameter()
]
)
]
)
]
),
Parameter()
]
)
]
)
train_model(model_binary, bce_loss, bce_loss_grad, generate_binary_data())Then we reasonably get
print(model_binary.predict([1, 0]))
print(model_binary.predict([0, 1]))
print(model_binary.predict([0, 1000]))
print(model_binary.predict([-5, 3]))
print(model_binary.predict([0, 0]))
>> 3.7310797619230176e-66
>> 0.9997781079343139
>> 0.9997781079343139
>> 0.9997781079343139
>> 0.23791579184662365Though this has reasonable runtime, it is somewhat slower than we would expect. This is because we have to call forward() and re-calculate the model inputs a lot in the call to backwards(). As such, have the following exercise:
Exercise 3: Add caching to our network. That is, on the call to forward(), the model should return the cached value from the previous call to forward() if and only if the inputs haven’t changed since the last call. Ensure that you run forward() again if the inputs have changed.
And that’s about it! We now have a working neural network framework in which we can train just a lot of interesting models (though not networks with nodes that feed into multiple other nodes. This isn’t too difficult to add — see the note in the discussion of the chain rule), though granted it’s a bit verbose. If you’d like to make it better, try some of the following:
Exercise 4: When you think about it, more “complex” nodes in our network (e.g. Linear layers) are really just “macros” in a sense — that is, if we had a neural net tree that looked, say, as follows:
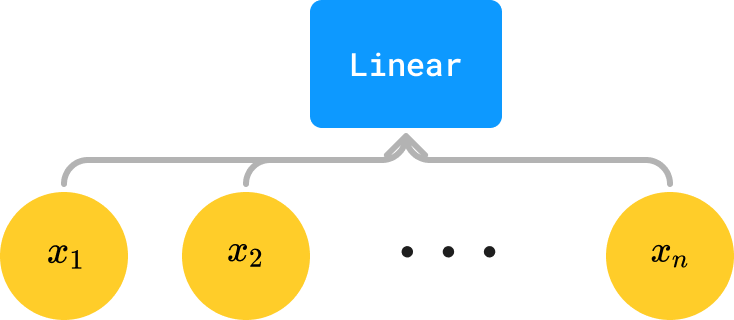
A linear classification model what you are really doing is this:
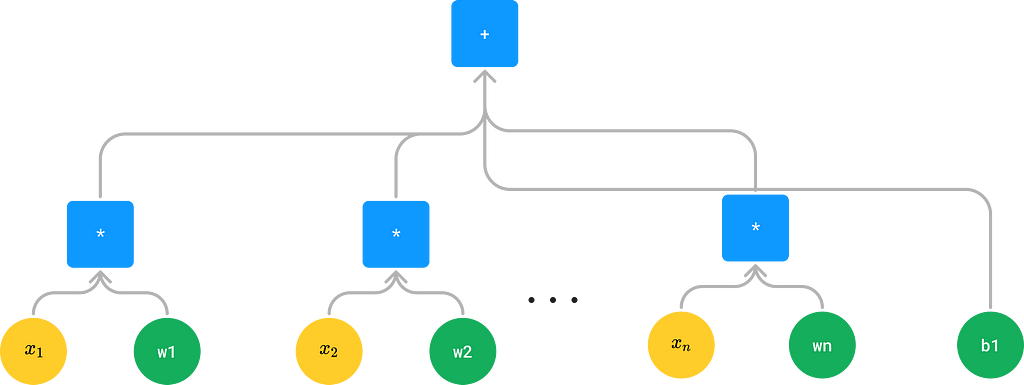
An equivalent formulation for our linear net In other words, Linear(inp) is really just a macro for a tree containing |inp| + 1 parameters, the first of which are weights in multiplication and the last of which is a bias. Whenever we see Linear(inp), we can thus substitute it for an equivalent tree composed only of elementary operations.
For this exercise, your job is thus to implement the Macro class. The class should be an Operation that recursively replaces itself with elementary operations
Note: this step can be done whenever, though it’s likely easiest to add a compile() method to the Operation class that you have to call before training (or add it to your existing method from Exercise 2). We can, of course, also implement more complex nodes in other (perhaps more efficient) ways, but this is still a good exercise.
Exercise 5: Though we don’t really ever need internal nodes to produce anything other than one number as their output, it is sometimes nice for the root of our tree (that is, our output layer) to produce something else (e.g. a list of numbers in the case of a Softmax). Implement the Output class and allow it to produce a Listof[float] instead of just a float. As a bonus, try implementing the SoftMax output.
Note: there are a few ways of doing this. You can make Output extend Operation, and then modify the NeuralNetNode class’ op() method to return a List[float] instead of just a float. Alternatively, you could create a new Node superclass that both Output and Operation extend. This is likely easier.
Note further that although these outputs can produce lists, they will still only get one derivative back from the loss function — the loss function will just happen to take a list of floats instead of a float (e.g. the Categorical Cross Entropy loss)
Exercise 6: Remember how earlier in the article we said that neural nets are just mathematical functions comprised of elementary operations? Add the funcify() method to the NeuralNetNode class that turns it into such a function written in human-readable notation (add parentheses as you please). For example, the neural net Add([Parameter(0.1), Parameter(0.2)]) should collapse to “0.1 + 0.2” (or “(0.1 + 0.2)”).
Note: For this to work, inputs should be named. If you did exercise 2, name your inputs in the compile() function. If not, you’ll have to figure out a way to name your inputs — writing a compile() function is still likely the easiest way.
Exercise 7: Modify our framework to allow nodes to have multiple parents. I will solve this in part 2.
That’s all for now! If you’d like to check out the code, you can look at this google colab that has everything (except for solutions to every exercise but #6, though I may add those in part 2).
Contact me at [email protected] for any inquiries.
Unless otherwise specified, all images are by the author.
But What is Backpropagation, Really? (Part 1) was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
But What is Backpropagation, Really? (Part 1)Go Here to Read this Fast! But What is Backpropagation, Really? (Part 1)
-
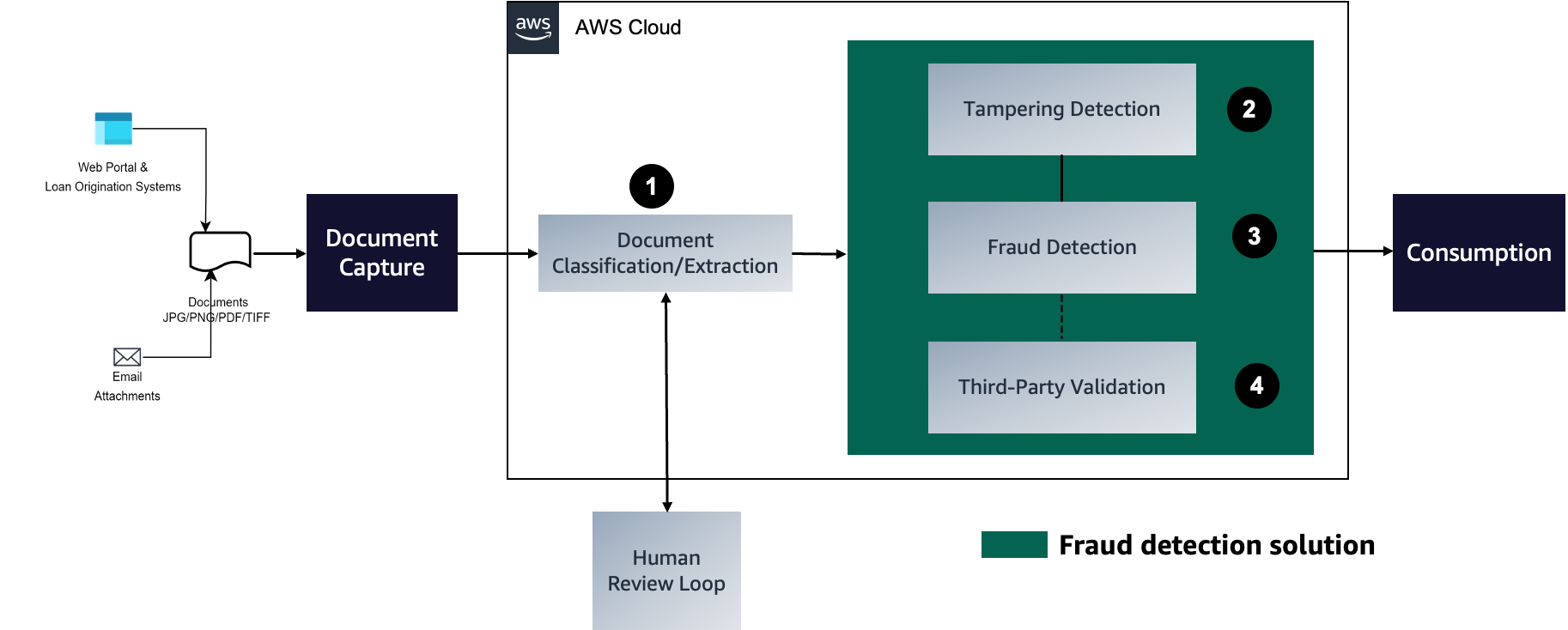
Automate mortgage document fraud detection using an ML model and business-defined rules with Amazon Fraud Detector: Part 3
 In the first post of this three-part series, we presented a solution that demonstrates how you can automate detecting document tampering and fraud at scale using AWS AI and machine learning (ML) services for a mortgage underwriting use case. In the second post, we discussed an approach to develop a deep learning-based computer vision model […]
In the first post of this three-part series, we presented a solution that demonstrates how you can automate detecting document tampering and fraud at scale using AWS AI and machine learning (ML) services for a mortgage underwriting use case. In the second post, we discussed an approach to develop a deep learning-based computer vision model […]Originally appeared here:
Automate mortgage document fraud detection using an ML model and business-defined rules with Amazon Fraud Detector: Part 3 -
Judge dismisses class-action antitrust case accusing Apple & Google of collusion
 A class-action lawsuit against Apple and Google suggested the company CEOs met in secret to collude on the suppression of the search market, but it has been dismissed by a Judge in California.
A class-action lawsuit against Apple and Google suggested the company CEOs met in secret to collude on the suppression of the search market, but it has been dismissed by a Judge in California.
Google and Apple accused of collusion to control search marketLawsuits against Apple and Google are a dime a dozen, but some leave the court as fast as they arrived. Many assume that there is some secret agreement beyond what is known between Apple and Google, and some believed it enough to take it to court.
According to a court filing seen by AppleInsider, California Judge Rita Lin has dismissed all claims made by the plaintiffs but has left the opportunity for one claim to be amended for reexamination. The plaintiffs have 30 days to submit their second amended complaint.
Judge dismisses class-action antitrust case accusing Apple & Google of collusionJudge dismisses class-action antitrust case accusing Apple & Google of collusion