Originally appeared here:
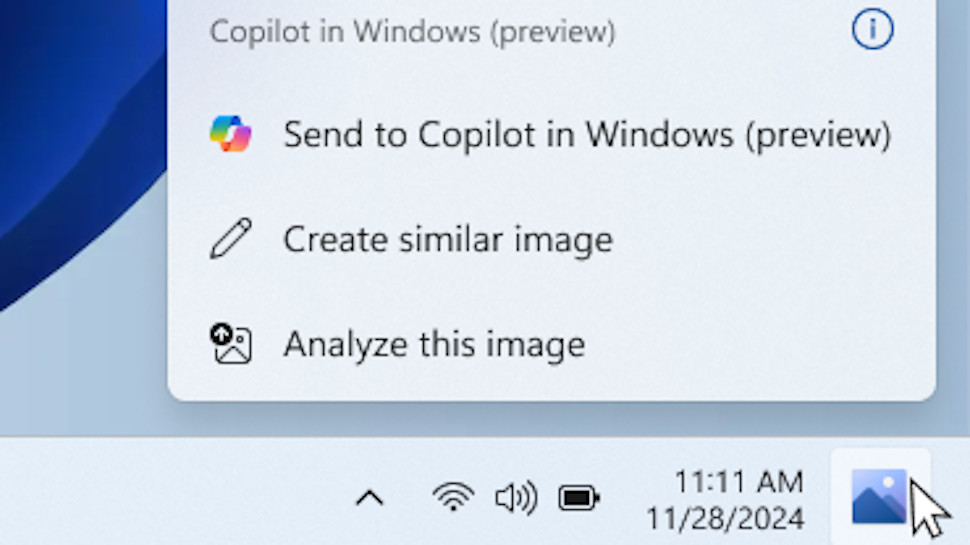
Microsoft is testing small but impactful changes to draw your attention to Copilot AI on the Windows 11 desktop

Originally appeared here:
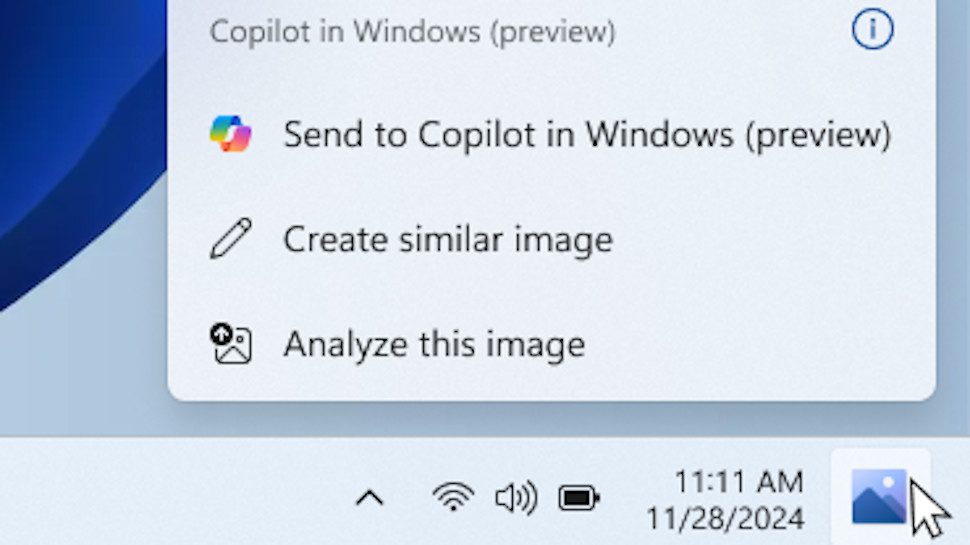
Microsoft is testing small but impactful changes to draw your attention to Copilot AI on the Windows 11 desktop
Ubunation, a web3 charity, has partnered with UNDER Lea’s TRUST, a non-profit organization dedicated to enhancing educational access in Kenya, to launch an innovative charitable fundraising campaign where 10,000 NFTs will be auctioned off to support the construction of a primary school in Nairobi. The “ULT Dream Careers Lion Charity Collection Campaign” will offer supporters […]
The post Web3 charity, Ubunation, to auction 10,000 NFTs to build a school in Kenya appeared first on CoinJournal.
Originally appeared here:
Web3 charity, Ubunation, to auction 10,000 NFTs to build a school in Kenya
Bearish sentiment around SOL has been dominant lately
Metrics seemed to support the possibility of an incoming rally though
The crypto-market’s present condition has restricted several crypt
The post Solana: SOL’s price might hit these targets within the next week appeared first on AMBCrypto.
Genesis sold GBTC to acquire BTC amid financial challenges and potential bankruptcy
Whales have been accumulating BTC ahead of the halving
Genesis, a crypto-lending company, has been grappli
The post Analyst makes ‘Bitcoin’s price to 10x post halving’ prediction because… appeared first on AMBCrypto.
Originally appeared here:
Milei Moneda investors eye profits as presale outshines Injective, Cardano
Failure rate went over 77% at one point of time on 5 April
Solana’s daily active user count, fees fell steadily over the week
Concerns over the Solana network’s capabilities heightened as th
The post Solana: Here’s the full story behind its ‘2nd straight day’ of txn ‘failures’ appeared first on AMBCrypto.



What if you were told there exists a new way to measure the relationship between two variables just like correlation except possibly better. More specifically, in 2020 a paper was published titled A New Coefficient of Correlation[1] introducing a new measure which equals 0 if and only if the two variables are independent, 1 if and only if one variable is a function of the other, and lastly has some nice theoretical properties allowing for hypothesis testing while practically making no assumptions about the data. Before we get into it, let us talk briefly about how more traditional correlation measures work.
There are few tools that exist to help understand data that are more commonly used (and misused) than the popular correlation coefficient. Formally known as Pearson’s r, the sample correlation coefficient taught in nearly every introductory statistics/business class is arguably the number one tool every data professional must be familiar with. The reasons for this are many, with one being it is both easy to use and interpret. As a reminder, the sample correlation coefficient measures the linear relationship between exactly two variables and can be calculated using the following formula.
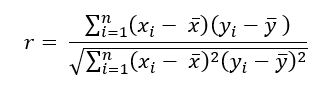
As a final reminder, this value can range from -1 to +1 with negative values implying an inverse linear relationship between the two variables being measured and a positive one implying the opposite. Notice the emphasis so far being placed on measuring linear relationships. Linear relationships can be understood as the shape of a relationship being somewhat traceable using a straight line.
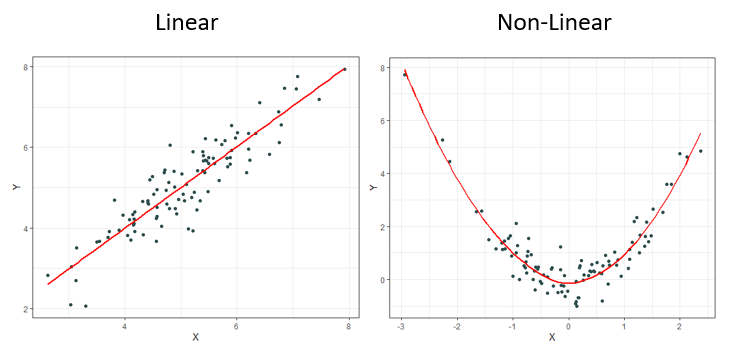
It should come as no surprise to most that it is rare to observe linear relationships in the real world. This is why other measures have been created over the decades such as Spearman’s ρ (rho) and Kendall’s τ (tau) to name a few. These newer measures are much better at identifying monotonic relationships and not just linear ones which makes them more robust since linear relationships are a specific type of monotonic relationship. Monotonic relationships can basically be understood as either always increasing or always decreasing.

Most of the time correlation is used, it is used to try and identify not necessarily a linear or monotonic relationship between two variables of interest, but instead identify if there exists any relationship. This creates problems, for if relationships are neither linear nor monotonic, these current measures do not work very well. Note how the plots below all display clearly strong relationships between two variables, but commonly used correlation techniques are only good at identifying monotonic ones.
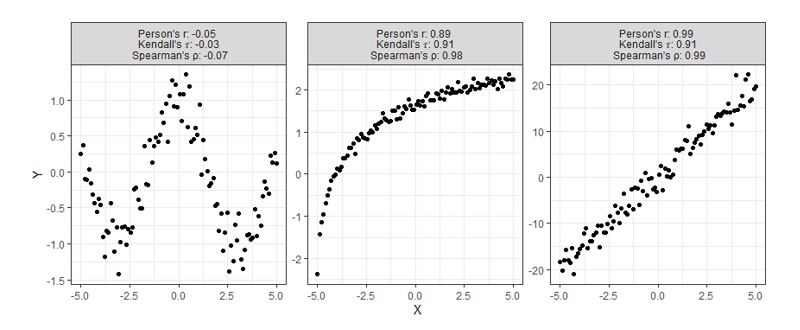
Despite having obvious shortcomings, these correlations are still being used to make many conclusions about all sorts of data. Is there any hope for identifying relationships that are even more complex than the ones shown above? Enter, the new coefficient ξ (pronounced “ksaai”).
One last note before moving on, a paper was published in 2022 titled Myths About Linear and Monotonic Associations[2] related to the issue of stating which popular measure of correlation is preferred for which type of data. Earlier, I suggested that Pearson’s r is most appropriate for linear measures while Spearman’s ρ and Kendall’s τ were better for monotonic data. While this rule is a popular belief and common practice amongst many data professionals, this paper makes a point to say that this is not necessarily the case, and that the opposite can in fact be true under certain circumstances.
Before introducing the formula, it is important to go over some needed prep-work. As we said earlier, correlation can be thought of as a way of measuring the relationship between two variables. Say we’re measuring the current correlation between X and Y. If a linear relationship does exist, it can be thought of as one that is mutually shared meaning the correlation between X and Y is always equal to the correlation between Y and X. With this new approach, however, we will no longer be measuring the linear relationship between X and Y, but instead our aim is to measure how much Y is a function of X. Understanding this subtle, but important distinction between traditional correlation techniques will make understanding the formulas much easier, for in general it is not necessarily the case anymore that ξ(X,Y) equals ξ(Y,X).
Sticking with the same train of thought, suppose we still wanted to measure how much Y is a function of X. Notice each data point is an ordered pair of both X and Y. First, we must sort the data as (X₍₁₎,Y₍₁₎),…,(X₍ₙ₎,Y₍ₙ₎) in a way that results in X₍₁₎ ≤ X₍₂₎≤ ⋯ ≤ X₍ₙ₎. Said clearly, we must sort the data according to X. We will then be able to create the variables r₁, r₂, … ,rₙ where rᵢ equals the rank of Y₍ᵢ₎. With these ranks now identified, we are ready to calculate.
There are two formulas used depending on the type of data you are working with. If ties in your data are impossible (or extremely unlikely), we have
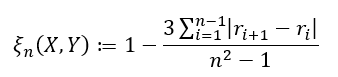
and if ties are allowed, we have
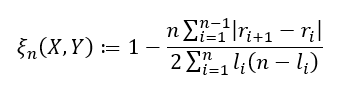
where lᵢ is defined as the number of j such that Y₍ ⱼ₎ ≥ Y₍ᵢ₎. One last important note for when ties are allowed. In addition to using the second formula, to obtain the best estimate possible it is important to randomly sort the observed ties in a way that one value is chosen to be ranked higher/lower over another so that (rᵢ₊₁ — rᵢ) is never equal to zero just as before. The variable lᵢ is then just the number of observations Y₍ᵢ₎ is actually greater than or equal to.
To not dive too much deeper into theory, it is also worth briefly pointing out this new correlation comes with some nice asymptotic theory behind it that makes it very easy to perform hypothesis testing without making any assumptions about the underlying distributions. This is because this method depends on the rank of the data, and not the values themselves making it a nonparametric statistic. If it is true that X and Y are independent and Y is continuous, then

What this means is that if you have a large enough sample size, then this correlation statistic approximately follows a normal distribution. This can be useful if you’d like to test the degree of independence between the two variables you are testing.
Along with the publishing of this new method, the R package XICOR was released containing a few relevant functions including one called xicor() which easily calculates the statistic ξ when X and Y vectors or matrices are provided as well as additional information like p-values for hypothesis testing. As with all articles I write, I will include original functions for R, Python, and Julia that you can simply copy and keep if you choose to. Here X and Y must either be a vector or an array, and for Python and Julia you may need to install the NumPy and Random package respectively.
## R Function ##
xicor <- function(X, Y, ties = TRUE){
n <- length(X)
r <- rank(Y[order(X)], ties.method = "random")
set.seed(42)
if(ties){
l <- rank(Y[order(X)], ties.method = "max")
return( 1 - n*sum( abs(r[-1] - r[-n]) ) / (2*sum(l*(n - l))) )
} else {
return( 1 - 3 * sum( abs(r[-1] - r[-n]) ) / (n^2 - 1) )
}
}
## Python Function ##
from numpy import array, random, arrange
def xicor(X, Y, ties=True):
random.seed(42)
n = len(X)
order = array([i[0] for i in sorted(enumerate(X), key=lambda x: x[1])])
if ties:
l = array([sum(y >= Y[order]) for y in Y[order]])
r = l.copy()
for j in range(n):
if sum([r[j] == r[i] for i in range(n)]) > 1:
tie_index = array([r[j] == r[i] for i in range(n)])
r[tie_index] = random.choice(r[tie_index] - arange(0, sum([r[j] == r[i] for i in range(n)])), sum(tie_index), replace=False)
return 1 - n*sum( abs(r[1:] - r[:n-1]) ) / (2*sum(l*(n - l)))
else:
r = array([sum(y >= Y[order]) for y in Y[order]])
return 1 - 3 * sum( abs(r[1:] - r[:n-1]) ) / (n**2 - 1)
## Julia Function ##
import Random
function xicor(X::AbstractVector, Y::AbstractVector, ties::Bool=true)
Random.seed!(42)
n = length(X)
if ties
l = [sum(y .>= Y[sortperm(X)]) for y ∈ Y[sortperm(X)]]
r = copy(l)
for j ∈ 1:n
if sum([r[j] == r[i] for i ∈ 1:n]) > 1
tie_index = [r[j] == r[i] for i ∈ 1:n]
r[tie_index] = Random.shuffle(r[tie_index] .- (0:sum([r[j] == r[i] for i ∈ 1:n])-1))
end
end
return 1 - n*sum( abs.(r[2:end] - r[1:n-1]) ) / (2*sum(l.*(n .- l)))
else
r = [sum(y .>= Y[sortperm(X)]) for y ∈ Y[sortperm(X)]]
return 1 - 3 * sum( abs.(r[2:end] - r[1:end-1]) ) / (n^2 - 1)
end
end
For a first look at the possible benefits of using this new formula, let us compare the calculated correlation values of a few simulated examples that highlight the key differences between each correlation method.

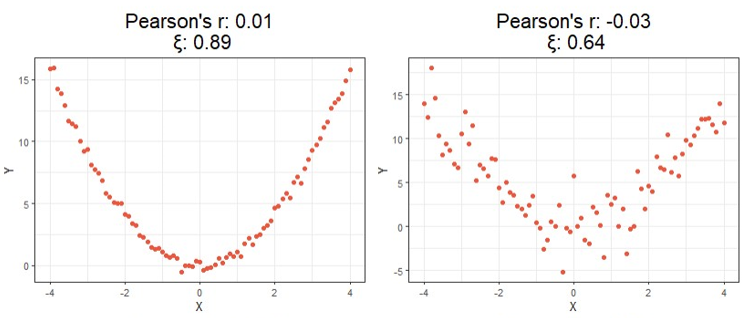
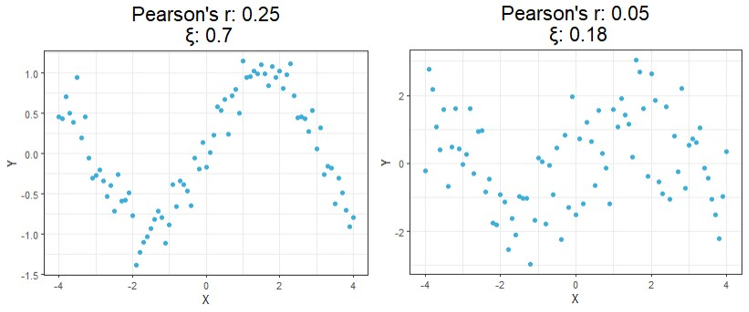
Starting at the top, we can see correlations using this new method no longer tell you the direction of the relationship since values can no longer be negative. As expected, however, this value is closer to 1 as the relationship strengthens and closer to 0 the more it weakens just like the aforementioned methods.
Moving on down is where things get exciting. It should be clear from the bottom four charts that this new approach is much more useful than traditional calculations at identifying significant relationships in general. Cases like these shown above are exactly the main motivation behind the research that led to this new formula since the second example shows Pearson’s r concludes there is no significant relationship between X and Y when there clearly exists a parabolic one, and the third example shows the same method concludes there’s a slight positive correlation when in reality the relationship appears to exhibit no upward trend.
Up to this point, we’ve only looked at simulated data. Let us now go over some visual results using this new correlation method with a real-world example. Suppose we want to measure the level of independence between brain signals and time.
The following data is a recording of brain activity measured in the form of BOLD signals using functional magnetic resonance imaging (fMRI) made available through the popular R package astsa. To provide more context, this dataset contains the average response observable in eight various brain locations in the cortex, thalamus, and cerebellum across five subjects. Each subject was exposed to periodic brushing of the hand for 32 seconds and then paused for 32 seconds resulting in a signal period of 64 seconds. Data was then recorded every 2 seconds for 256 seconds total (n = 128).
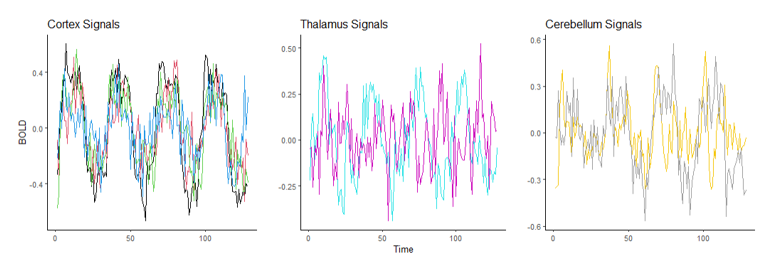
Suppose we wish to measure which of these three parts of the brain is most likely a function of time implying they are most involved when performing the prescribed stimulation. From the visual above, it appears that the Cortex signals are the least noisy, and one of the Thalamus’ signals are the noisiest, but let us quantify this using our new correlation statistic. The following table shows the correlation value of each of the eight measurements using the popular Pearson’s r and the new correlation ξ.
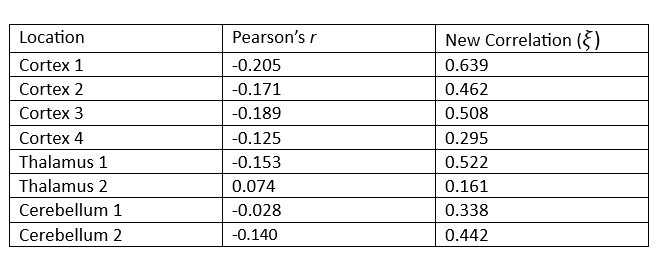
The table above reveals the common method for correlation consistently shows each of these relationships to be negative or approximately zero implying there is little to no observable relationship, and if there is one it exhibits a downward trend. This is clearly not the case since some of these wavelengths exhibit visibly strong relationships with time, and all of them appear to have no trend.
Furthermore, the new correlation values do a much better job identifying which location is least noisy, which is the main point of this analysis. The results show that parts of the Cortex are most notably being used during the period of stimulation since those correlation values are the highest on average, but there are also parts of the Thalamus that appear involved as well, a result not so easily detectable using the standard approach.
There is more that can be done to continue the analysis we started, such as perform an official hypothesis test of independence using the asymptotic theory presented earlier, but the purpose of this report was to simply introduce the new measure and showcase how simple these computations can be and how these results can be used. If you are interested in learning more about the pros and cons of this approach, I would encourage you to read the official publication introducing the method found in the references below.
This new approach is far from perfect, but it was created as a means of solving some of the most notable issues with the currently accepted approach. Since discovering it, I have been using it for my own personal research and it has proven very helpful.
Unless otherwise noted, all images, plots, and tables are by the author.
[1] S. Chatterjee, A New Coefficient of Correlation (2020), Journal of the American Statistical Association.
[2] E. Heuvel and Z. Zhan, Myths About Linear and Monotonic Associations (2022), The American Statistician.
A New Coefficient of Correlation was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
A New Coefficient of Correlation

Nikola Milosevic (Data Warrior)

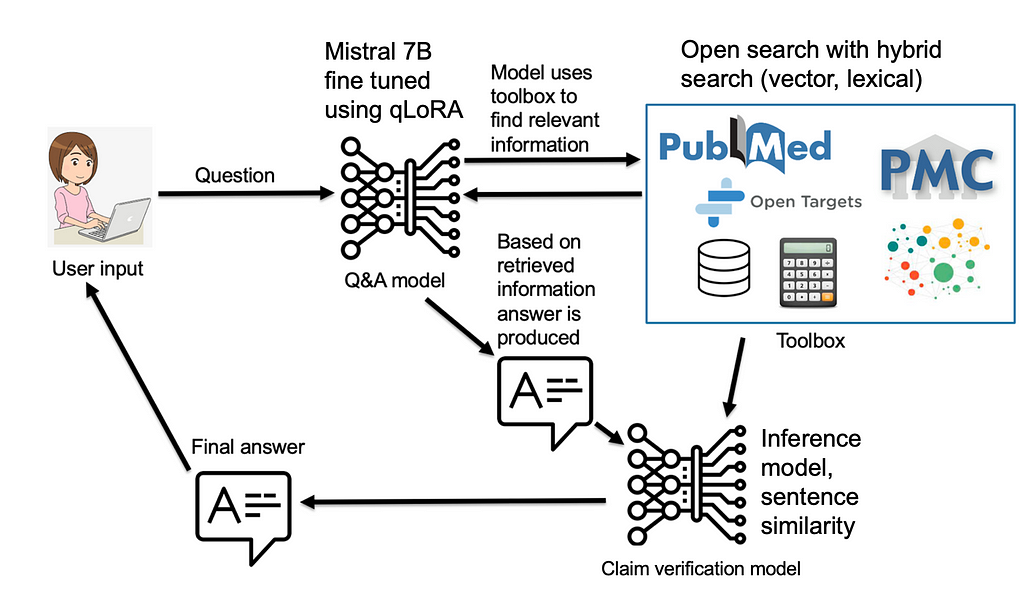
During the past year, I have been working on two projects dealing with hallucination detection of large language models and verifying claims produced by them. As with any research, especially one looking at verification of claims, it led to quite a bit of literature review, in which I have learned that a lot of authors, the task of verifying whether some claim is based on evidence from a reputable source (e.g. previous scientific publication, encyclopedia article, etc.) is often called fact-checking (examples of such publications include Google Deep Mind, University of Pennsylvania, University of Washington, Allen Institute for AI, OpenAI and others). Even datasets, such as SciFact, have factuality in the name.
I assume that calling some metric in large language models factuality goes back to the LaMDA paper by Google, which, published in February 2022, is to the best of my knowledge the first mention of such a metric in LLM. Before one could find occasional instances of fact-checking, like for example in a SciFact paper (from 2020), but LaMDA was the first mention related to LLMs. In the LaMDA paper, this metric was called factual grounding, which is a way better name than the later simplified versions, such as “factuality” or “faithfulness”. In this article, I would like to discuss why the name of the metric should be claim verification, and why I think names like faithfulness, factuality, and fact-checking are wrong from both practical and philosophical standpoints.

Let’s examine what is the base of the task. Given the claim that has been produced by a large language model, we are checking whether it is grounded in evidence from some source. This source can be an article from the literature, but it can be, also, some less formal source, such as encyclopedias, the internet, or any other kind of retrieved information source. Quite often, this task goes back to natural language entailment or natural language inference, where we find whether the claim can be derived from the evidence piece of text. However, there are other approaches, using textual similarity, or other large language models with various kinds of prompts. The task is always whether the generated claim is grounded in the evidence or knowledge we have of the world today. The task can be viewed similarly to generating a literature review part of an article or thesis, and verifying whether the referenced articles support the author’s claims. Of course, we are talking here about automating this task.
Now, what is the problem with naming this task fact-checking or measuring the factuality of the model?
From a philosophical standpoint, it is hard for us to know what the fact is. With all the best intentions, in their pursuit of truth, scientists often write in their publications things that may not be factual, and that will also easily pass peer review. I am here to emphasize, that people do their best effort, especially in scientific publishing, to be as factual as possible. However, that often fails. The publications may contain distorted, exaggerated, or misinterpreted information due to various factors, such as cultural biases, political agendas, or lack of reliable evidence. Often, science is just slowly and naturally moving toward facts by producing new evidence and information.
We had quite a few events in history, in which the common consensus in the field was set, in order to be shaken from its foundation. Think about for example Copernicus: Before Copernicus, most people believed that the Earth was the center of the universe and that the sun, the moon, and the planets revolved around it. This was the geocentric model, which was supported by the teachings of the Catholic Church and the ancient Greek philosopher Aristotle. However, Copernicus, a Polish astronomer and mathematician, proposed a radical alternative: the heliocentric model, which stated that the Earth and the other planets orbited the sun. He based his theory on mathematical calculations and observations of the celestial motions. His work was published in his book On the Revolutions of the Heavenly Spheres in 1543, shortly before his death. Although his theory faced strong opposition and criticism from the religious authorities and some of his contemporaries, it gradually gained acceptance and influence among other scientists, such as Galileo, Kepler, and Newton. The heliocentric model paved the way for the development of modern astronomy and physics and changed the perception of the Earth’s place in the cosmos.
A similar happened with Darwin. Before Darwin, most people believed that the living species were created by God and remained unchanged since their origin. This was the creationist view, which was based on the biblical account of Genesis and the natural theology of the British naturalist John Ray. However, Darwin, an English naturalist and geologist, proposed a radical alternative: the theory of evolution by natural selection, which stated that the living species descended from common ancestors and changed over time due to environmental pressures and the survival of the fittest. There are several more examples, such as Einstein’s relativity, gravity, Khan’s theory on scientific revolutions, and many others.
These events in history are called paradigm shifts, in which the base paradigm in certain fields was significantly shifted. Paradigm shifts may be fairly rare, however, we have as well many common beliefs and myths a lot of people believe, such as that the Great Wall of China can be seen from space, that Napoleon was short, or that Columbus discovered America, which can be found even in scientific articles or books written on the topics, despite them being untrue. People keep citing and referencing works containing this information and they still propagate. Therefore, checking whether the evidence in the referenced literature supports the claim is not a good enough proxy for factuality.
Providing references to the evidence we have for some claims is our best method for supporting the claim. Checking supporting evidence often requires also examining whether the reference is reputable, peer-reviewed, published in a reputable journal, year of publication, etc. Despite all these checks, the information may still be a victim of a paradigm shift or newly generated hypothesis and evidence for it and therefore incomplete and obsolete. But it is our best tool, and we should keep using it. Provided examples illustrate how verification of sources is not always fact-checking, but rather a way of approaching and evaluating claims based on the best available evidence and the most reasonable arguments at a given time and place. However, verification of sources does not imply that all claims are equally valid or that truth is relative or subjective. Verification of sources is a way of seeking and approximating the truth, not denying or relativizing it. Verification of sources acknowledges that truth is complex, multifaceted, and provisional, but also that truth is real, meaningful, and attainable.
Therefore, instead of using the term fact-checking, which suggests a binary and definitive judgment of true or false, we should use the term claim verification, which reflects a more nuanced and tentative assessment of supported or unsupported, credible or dubious, consistent or contradictory. Claim verification is not a final verdict, but a continuous inquiry, that invites us to question, challenge, and revise our beliefs and assumptions in light of new evidence, new sources, and new perspectives.
The right term for the task, in my opinion, is claim verification, as that is what we are doing, we are verifying whether the claim is grounded in the evidence from the referenced article, document, or source. There have been papers published naming the task claim verification (e.g. check this paper). So, I would like to try to call on authors working in this area, to avoid naming their metrics factuality, or fact-checking, but rather call it verifiability, claim verification, etc. I can assume that fact-checking from the marketing perspective looks better, but it is a bad name, not giving the proper treatment and credit to the pursuit of facts and truth in science, which is a much more complex task.
There is a big risk in that name from a practical point of view as well. In a situation where we “absolutely trust” some source to be “absolutely factual”, we lose the ability to critically examine this claim further. No one would have the courage or ability to do so. The core of science and critical thinking is that we examine everything in the pursuit of truth. On top of that, if AI in its current form, would measure factfulness and check facts only based on current knowledge and consensus, we are falling into the risk of halting progress and becoming especially averse to future paradigm shifts.
However, this risk is not only within sciences. The same argument of what is fact and excluding critical thinking from even whole educational systems is a common characteristic of authoritarian regimes. If we would less critically asses what is served to us as facts, we may fall victim to future authoritarians who would utilize it, and integrate their biases into what is considered “fact”. Therefore, let’s be careful of what we call fact, as in most cases it is a claim. A claim may be true based on our current understanding of the world and the universe, or not. Also, whether a claim is correct or not may change with the new evidence and new information that is discovered. One of the big challenges of AI systems, and especially knowledge representation, in my opinion, will be: how to represent knowledge that is our current understanding of the Universe and that will stay up-to-date over time.
Unless otherwise noted, all images are by the author.
Fact-checking vs claim verification was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Fact-checking vs claim verification
Go Here to Read this Fast! Fact-checking vs claim verification
Go here to Read this Fast! ZA Bank launches banking solutions for stablecoin issuers in Hong Kong
Originally appeared here:
ZA Bank launches banking solutions for stablecoin issuers in Hong Kong