Go here to Read this Fast! Bitcoin drives record $2.4b weekly digital asset investment inflows
Originally appeared here:
Bitcoin drives record $2.4b weekly digital asset investment inflows
Go here to Read this Fast! Bitcoin drives record $2.4b weekly digital asset investment inflows
Originally appeared here:
Bitcoin drives record $2.4b weekly digital asset investment inflows
In a strategic move ahead of the upcoming general elections, South Korea’s ruling party, the People Power Party (PPP), has announced plans to push for a further two-year delay in the implementation of crypto taxation, local media reported Feb. 19. Party officials announced the intention to explore the delay as a key campaign promise during […]
The post South Korea’s ruling party proposes delay in crypto taxation as election pledge appeared first on CryptoSlate.
Originally appeared here:
South Korea’s ruling party proposes delay in crypto taxation as election pledge

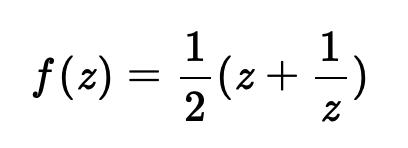
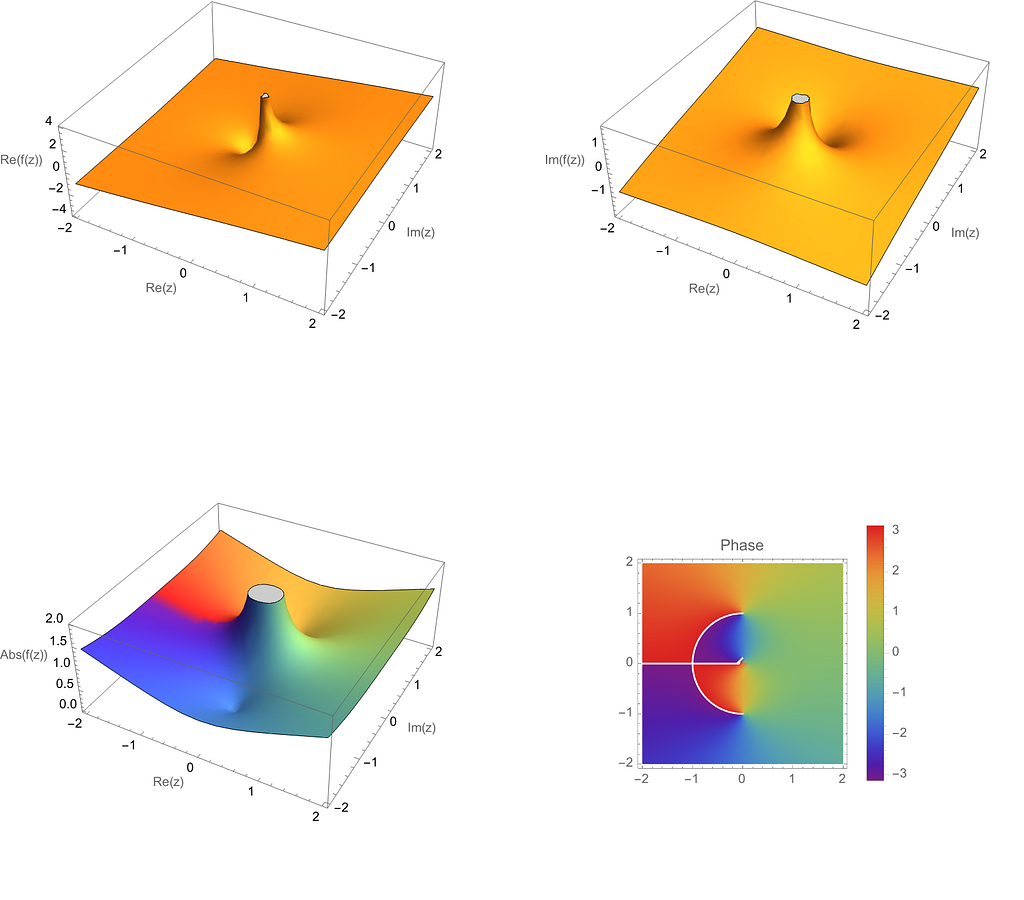
Today I was pouring through Complex Variables and Analytic Functions by the esteemed Fornberg and Piret, trying my best to wrap my mind around how complex-valued functions behave. Mentally vizualization such functions is extra difficult since they take a real and an imaginary input, and outputs two components as well. Therefore, a single 3-D plot is not sufficient to see how the function behaves. Rather, we have to split such a visualization into separate plots of the imaginary and real parts, or alternatively by magnitude and argument, or angle.
I wanted to be able to play around with any function I could think of, drag and zoom around its plots, and explore it in visual detail to understand how it resulted from the equation. For such a task, Wolfram Mathematica is an excellent starting tool.
plotComplexFunction[f_]:=Module[{z,rePlot,imPlot,magPlot,phasePlot},z=x+I y;
rePlot = Plot3D[Re[f[z]],{x,-2,2},{y,-2,2},AxesLabel->{"Re(z)","Im(z)","Re(f(z))"},Mesh->None];
imPlot = Plot3D[Im[f[z]],{x,-2,2},{y,-2,2},
AxesLabel->{"Re(z)","Im(z)","Im(f(z))"},
Mesh->None];
magPlot = Plot3D[Abs[f[z]], {x, -2, 2}, {y, -2, 2},
AxesLabel -> {"Re(z)", "Im(z)", "Abs(f(z))"},
Mesh -> None,
ColorFunction -> Function[{x, y, z}, ColorData["Rainbow"][Rescale[Arg[x + I y], {-Pi, Pi}]]],
ColorFunctionScaling -> False];
phasePlot=DensityPlot[Arg[f[z]],{x,-2,2},{y,-2,2},
ColorFunction->"Rainbow",
PlotLegends->Automatic,
AxesLabel->{"Re(z)","Im(z)"},
PlotLabel->"Phase"];
GraphicsGrid[{{rePlot,imPlot},{magPlot,phasePlot}},ImageSize->800]];
f[z_]:=(1/2)*(z+1/z);
plotComplexFunction[f]
https://github.com/dreamchef/complex-functions-visualization
https://github.com/dreamchef/complex-functions-visualization
I wrote the above Mathematica code to produce a grid of plots showing the function in both ways just described. On the top, the imaginary and real parts of the function
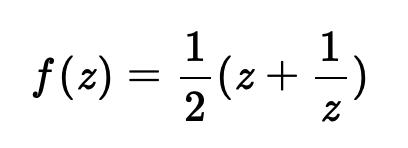
are shown, and on the bottom, and the magnitude, and the phase shown in color:
After playing around with a few functions using this code and convincing myself they made sense, I was interested in getting the same functionality in Python, to connect it to my other mathematical programming projects.
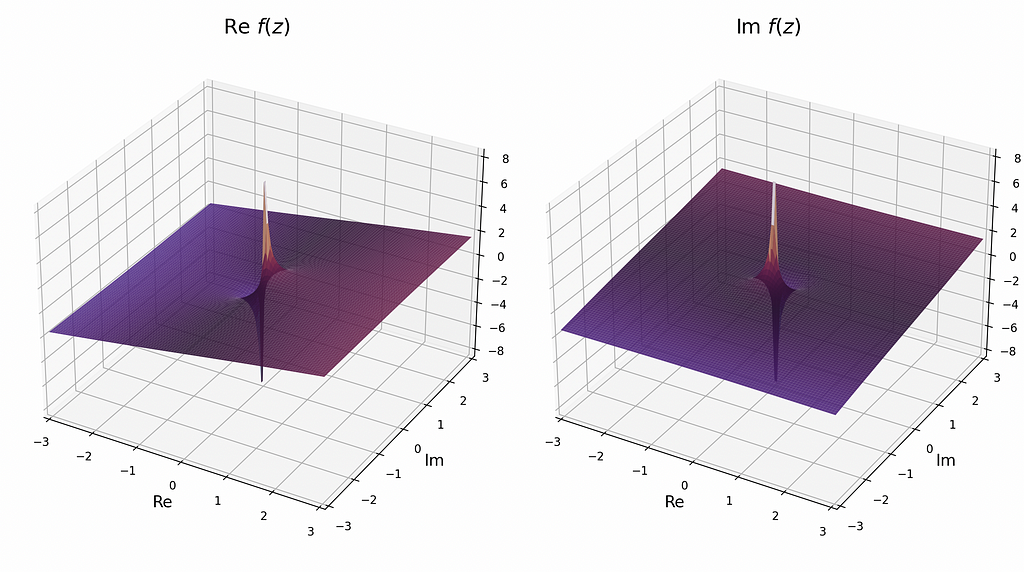
I found an excellent project on GitHub (https://github.com/artmenlope/complex-plotting-tools) which I decided to use as a starting point, and potentially contribute to in the future. The repo provided a very easy interface for plotting complex-valued functions in a variety of ways. Thanks https://github.com/artmenlope! For example, after importing numpy, matplotlib, and the repo’s cplotting_tools module defining the function and calling cplt.complex_plot3D(x,y,f,log_mode=False) produces the following:
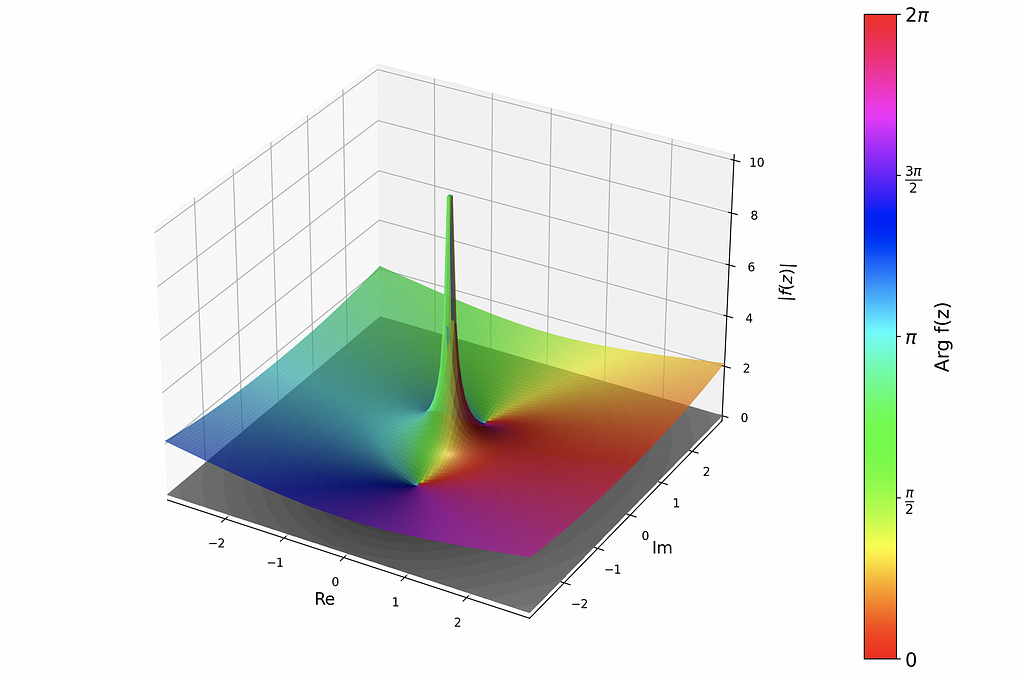
These are all for the same f(z) as above. To view the side-by-side imaginary and real parts of the function, use cplot.plot_re_im(x,y,f,camp=”twilight”,contour=False,alpha=0.9:
Additionally, the library provides other cool ways to study functions, including a stream plot:
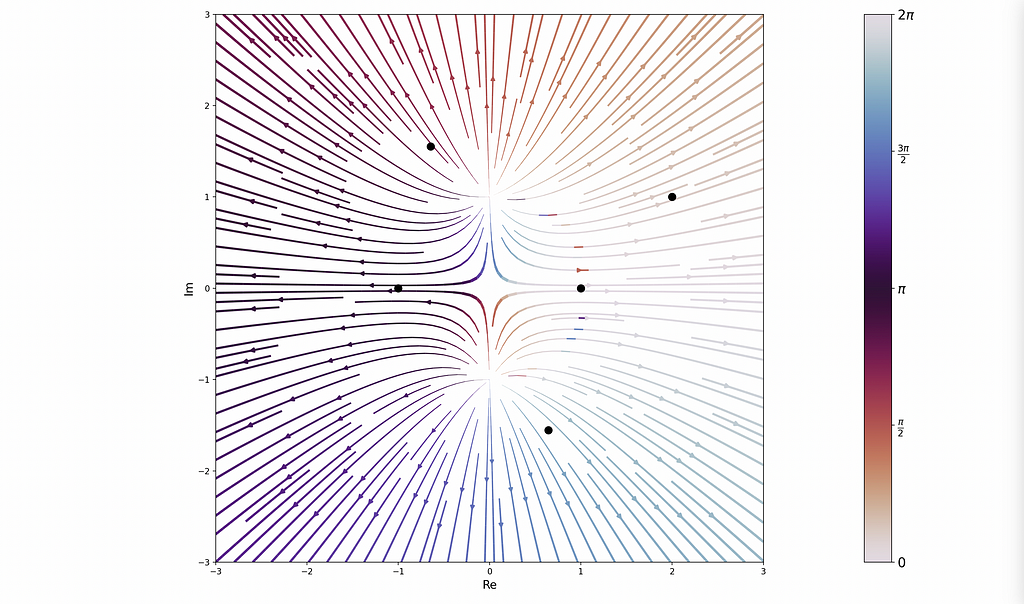
The library shows a lot of promise and is relatively easy to use! It does require a pts variable to be defined that encodes the poles and zeros of the given function. Wolfram does not require this because it computes the locations of these points under the hood. It would save a lot of effort for the user if complex-plotting-tools had this functionality as well. I plan to implement this is into the module in the near future.
In the meantime, have fun plotting with Wolfram and Python, and share your thoughts and questions in comments below, connect with me on LinkedIn or collaborate with me on GitHub!
Unless otherwise noted, all images were created by the author.
Visualizing Complex-Valued Functions Using Python and Mathematica was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Visualizing Complex-Valued Functions Using Python and Mathematica
Go Here to Read this Fast! Visualizing Complex-Valued Functions Using Python and Mathematica

Originally appeared here:
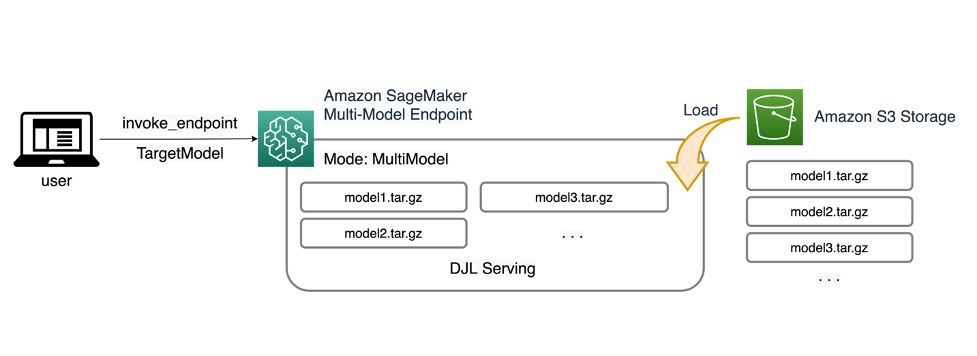
Run ML inference on unplanned and spiky traffic using Amazon SageMaker multi-model endpoints


Originally appeared here:
Use Amazon Titan models for image generation, editing, and searching
Go Here to Read this Fast! Use Amazon Titan models for image generation, editing, and searching



The global agreement, announced on Monday, is a multi-year agreement that will see Beats provide custom versions of Beats headphones created specifically for the teams.
Eight teams have been selected for the custom headphone treatment in 2024, including Atlanta United, Columbus Crew, Inter Miami, LAFC, Nashville SC, NYCFC, St. Louis City SC, and Toronto FC. Others will be added to the roster in the future.
Go Here to Read this Fast! MLS teams to get custom Beats headphones in a multi-year brand deal
Originally appeared here:
MLS teams to get custom Beats headphones in a multi-year brand deal



On February 16, Jenifer Lopez — also known as J Lo — released her ninth studio album, titled “This is Me… Now.” The album is a spiritual sequel to her 2002 album “This is Me… Then.”
Lopez, known for hits like “I’m Real” and “Love Don’t Cost A Thing,” has partnered with Apple Music to offer an exclusive performance to celebrate the release of the new album. The performance, which will take place on February 21 at 7:00 PM PT / 10:00 PM ET, was announced on Monday on social media platform X.

Originally appeared here:
Microsoft is adding support for AMD’s neural processors in Windows – here’s why it matters
Go Here to Read this Fast! Notorious NSO Group exploits flaw to send malicious messages and more
Originally appeared here:
Notorious NSO Group exploits flaw to send malicious messages and more