Go here to Read this Fast! Ethereum price approaching $3k, supporters accumulating
Originally appeared here:
Ethereum price approaching $3k, supporters accumulating
Go here to Read this Fast! Ethereum price approaching $3k, supporters accumulating
Originally appeared here:
Ethereum price approaching $3k, supporters accumulating
Go here to Read this Fast! MetaMask integrates Blockaid security alerts into platform
Originally appeared here:
MetaMask integrates Blockaid security alerts into platform
As the price of Bitcoin [BTC] soared to new heights in recent days, Ethereum [ETH] followed suit. On the 19th of February, ETH reached its highest price in 22 months, hitting $2,980.
This is the f
The post Ethereum’s rally spurs ‘Altseason’ hopes, but skeptics say… appeared first on AMBCrypto.



Ethereum co-founder Vitalik Buterin has expressed his excitement about the potential of AI-assisted formal verification of code and bug finding.
Go here to Read this Fast! Vitalik Buterin Highlights Potential Use Case of AI On Ethereum
Originally appeared here:
Vitalik Buterin Highlights Potential Use Case of AI On Ethereum



2024 has everything to be the biggest year in the history of the Ethereum ecosystem.
Originally appeared here:
Bernstein Uber-Bullish On Ethereum: Is Ether The Next ‘Institutional Darling’ With ETH Price Smashing New All-Time High?
Humanity Protocol emerges from stealth with Human Institute, Polygon Labs and Animoca Brands partnership. The protocol provides for a privacy-preserving alternative to the more invasive biometric methods such as iris scans. Human Institute has announced the launch of Humanity Protocol, a zkEVM Layer-2 blockchain protocol that leverages the Polygon CDK to offer a new palm […]
The post Polygon Labs, Animoca Brands partner with Human Institute to launch ZKP-powered palm recognition appeared first on CoinJournal.
Originally appeared here:
Polygon Labs, Animoca Brands partner with Human Institute to launch ZKP-powered palm recognition
Go here to Read this Fast! Ethereum hits $3k on Dencun, spot ETH ETF anticipation
Originally appeared here:
Ethereum hits $3k on Dencun, spot ETH ETF anticipation
This is a take on the Vehicle Routing Problem problem, but adapted to the air transport networks, namely the Origin Destination-to-Leg problem.

A little background first: Airlines are constantly faced with the question of how to address demand between city-pairs — do they open a direct connection, or provide connecting itineraries so that the demand is channeled through one or more hubs? The latter is of course preferable from a passenger perspective, but is more costly for the airline and therefore riskier — what if the flight is not filled? Operating a route is very expensive. In other words, we are trying to do this*:
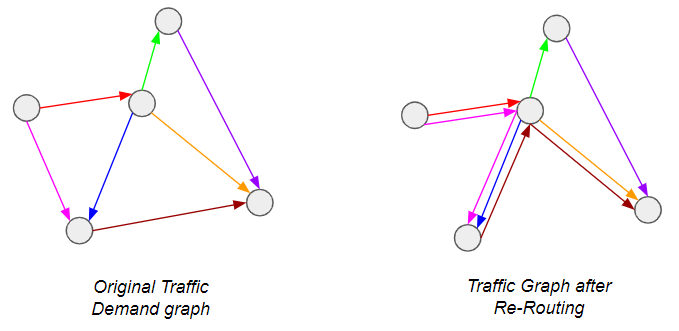
*Graph theory enthusiasts will recognize this as a special case of the Graph Sparsification problem, which has seen considerable attention lately.
The industry typically addresses this using so-called itinerary choice models, which are simply probabilistic models to determine which routings passengers will prefer on the basis of number of connections, route length, flight times etc… While this works well when the network shape is already fixed, deciding which routes to open is more complicated. This is because there are a number of routes which are only viable if they can capture enough connecting traffic from other sources — this in turn only occurs if there are no direct routes to serve said traffic. In other words, the status of each route is dependent on the status of neighboring routes, turning this into a combinatorial problem.
This is precisely the kind of problem that Mixed Integer Programs (MIP) are designed for! Specifically, we will formulate a problem to reflect the following behaviors: Network Flow Conservation and Edge Activation Costs to enforce sparsification.
For the rest of this article, I will use a toy example as illustration. To completely describe the problem, we need the following inputs:
A dense Origin-Destination bidirectional graph G = (V, E), with n vertices V and m edges E. Each edge has as attribute the Origin-Destination demand (O) and the distance between each city-pair (Distance). Typically, the demand follows a pareto distribution, where a few edges have high demand and the rest have low demand*:

*Graph generated by randomly instantiating the coordinates of the nodes and their population. Using the so-called gravity model for transport, a realistic demand profile can then be obtained. For more information, see link
Depending on the edge distance and typical vehicle type that would be assigned, each edge would have the following cost properties:
Bear in mind that both Costₚₐₓ and Costₘᵢₙ are m × 1 vectors (one per edge), and both costs scale linearly with distance.
With this, we have everything we need to design our MIP. As you might have guessed, the idea is to minimize the cost function of the system while respecting the network flow constraint.
This is a well-known condition, which states that the inflow and outflow of each vertex must be balanced, unless it is a source or sink:
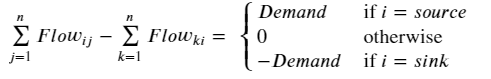
Here (i, j, k) are vertex indices. I’m personally not a big fan of this type of notation, and prefer the equivalent expression using the concept of the edge-incidence matrix from graph theory. This is usually denoted by the n × m matrix B, where each row entry is zero except at the incidence vertices for the corresponding edge, which are 1 & -1 to represent the source & sink:

If we initialize an m × m variable matrix (let’s call it R for Itinerary Routing — see Figure 1) to represent the flow routing for each demand edge in G, we can equivalently formulate the above condition by:
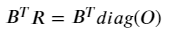
Where diag(O) is an m × m matrix with each diagonal entry corresponding to the demand from edge i. If you multiply out any row i of the RHS, it immediately becomes obvious why any R that satisfies this equation is valid from a flow conservation perspective.
Note however that both the B and R are directional. In the context of our cost function, we don’t really care whether some flows are negative — we just want the absolute, total number of passengers flowing along the edge i in order to quantify the cost of carrying them. To represent this, we can define the m × 1 leg vector L:
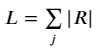
With these definitions, we have a function mapping O → L that is compatible with the network flow conservation principle. From hereon, L represents the total passenger volume on each edge.
This is the heart of the problem! Consider that if Costₘᵢₙ=0, the solution would be trivial, with L mapping to O on a one-to-one basis. This is because any alternative routing would necessarily cover a longer distance than the direct route, so that the cheapest option would always be the latter. However, in the presence of Costₘᵢₙ, there is a trade-off between the △Cost incurred by longer distance travelled vs. △Cost incurred through edge-activation. In other words, we need the cost profile for each edge to be:
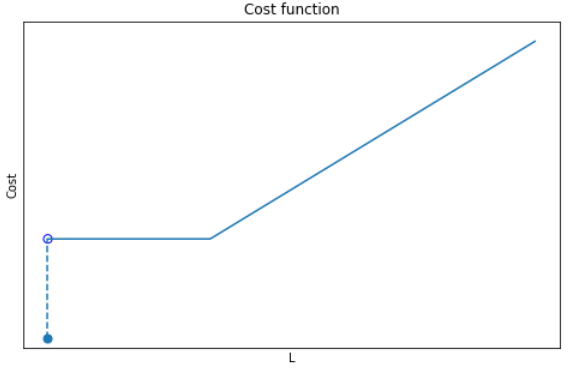
There are 3 parts to this function:
If it were not for the zero-point discontinuity, this would have been a pretty simple problem to solve. Instead, we have a non-convex, combinatorial problem because there is a sudden shift in behavior depending on whether the number of passengers along an edge is zero or not. In this situation, we need an activation (binary) variable to tell the algorithm which condition to follow. Using the big-M approach, we can formulate this as follows:
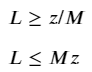
Where the m × 1 vector of binary variables z (i.e. z ∈ [0,1]) indicates if a route is open or not, and a very large scalar variable M. If you’re not familiar with the big-M method, you can read up on it here. In this context, it simply enforces the following conditions:
Ideally, we would have liked to simply multiply the cost function by this activation variable to tell it which cost behavior to follow. However, this would make the constraint non-linear and very complicated to solve. Instead, we can use Big-M again, this time to linearize the problem while getting the same effect:
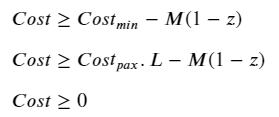
Combining the cost minimization objective with the ≥ inequalities, we basically end up with a minmax problem where:
And there we have it! The complete formulation of the problem is shown:
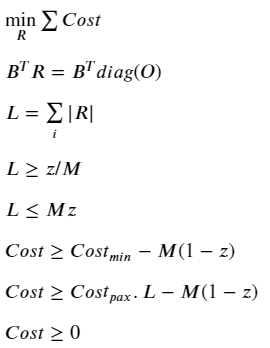
We now only have to plug in some numbers to see the magic happen.
It should be clear from the description that the minimum threshold is the main input of interest here, because it defines the degree of sparsification. It’s interesting to see the impact using progressively higher thresholds:
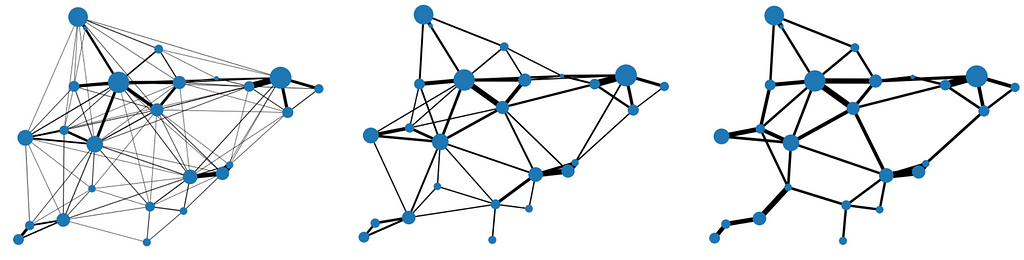
Notice how, no matter the threshold, the graph remains connected — this is a result of the network flow conservation principle, to ensure all demand is satisfied. Another neat way to visualize it is to look at the demand distribution along edges:
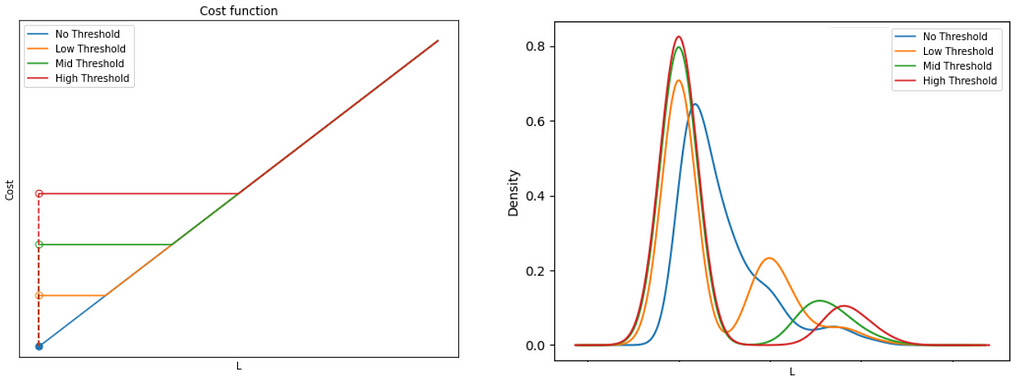
Here we see how the higher the threshold, the higher the level of consolidation (fewer routes with higher volume of traffic), and a correspondingly high number of routes with no traffic.
This was a simple introduction to what is in reality a very complex problem (there is far more nuance to airline networks than just minimum threshold costs). Still, it demonstrates one of the core behaviors of real networks, while giving a basic introduction to some key concepts for formulating MIPs. The codes for this are on my Github, feel free to give it a try.
If you actually try to run it, you’ll soon notice that solve time scales exponentially with the number of vertices in the graph. This is especially the case if you solve it with cvxpy — a common (but rudimentary) open source python library for simple optimization problems. That said, even the sophisticated commercial solvers soon run into their limits. This is the unescapable truth of combinatorial problems; they scale poorly, and are often impractical beyond a certain problem size.
In the next article, I will introduce a way to try to abstract away some of the complexity by using Graph Neural Networks as surrogate models.
All images unless otherwise stated are by me, the author.
An Introduction to Air Travel Network Optimization Using Mixed Integer Programming was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
An Introduction to Air Travel Network Optimization Using Mixed Integer Programming


PCA is an important tool for dimensionality reduction in data science and to compute grasp poses for robotic manipulation from point cloud data. PCA can also directly used within a larger machine learning framework as it is differentiable. Using the two principal components of a point cloud for robotic grasping as an example, we will derive a numerical implementation of the PCA, which will help to understand what PCA is and what it does.
Principal Component Analysis (PCA) is widely used in data analysis and machine learning to reduce the dimensionality of a dataset. The goal is to find a set of linearly uncorrelated (orthogonal) variables, called principal components, that capture the maximum variance in the data. The first principal component represents the direction of maximum variance, the second principal component is orthogonal to the first and represents the direction of the next highest variance, and so on. PCA is also used in robotic manipulation to find the principal axis of a point cloud, which can then be used to orient a gripper.

Mathematically, the orthogonality of principal components is achieved by finding the eigenvectors of the covariance matrix of the original data. These eigenvectors form a set of orthogonal basis vectors, and the corresponding eigenvalues indicate the amount of variance captured by each principal component. The orthogonality property is essential for the interpretability and usefulness of the principal components in reducing dimensionality and capturing the key patterns in the data.
As you know, the sample variance of a set of data points is a measure of the spread or dispersion of the values. For a random variable X with n data points, the sample variance s² is calculated as:
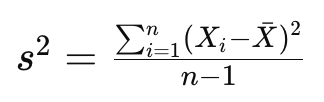
where barred X is the mean of the dataset. The division by n-1 instead of n is done to correct for bias in the estimation of the population variance when using a sample. This correction is known as Bessel’s correction and helps to provide an unbiased estimate of the population variance based on the sample data.
If we now assume our datapoints to be presented in an n-dimensional vector, X² will result in an nxn matrix. This is known as the sample covariance matrix. The covariance matrix is hence defined as

With this, we can implement this in Pytorch using its built-in PCA functions:
import torch
from sklearn.decomposition import PCA
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# Create synthetic data
data, labels = make_blobs(n_samples=100, n_features=2, centers=1,random_state=15)
# Convert NumPy array to PyTorch tensor
tensor_data = torch.from_numpy(data).float()
# Compute the mean of the data
mean = torch.mean(tensor_data, dim=0)
# Center the data by subtracting the mean
centered_data = tensor_data - mean
# Compute the covariance matrix
covariance_matrix = torch.mm(centered_data.t(), centered_data) / (tensor_data.size(0) - 1)
# Perform eigendecomposition of the covariance matrix
eigenvalues, eigenvectors = torch.linalg.eig(covariance_matrix)
# Sort eigenvalues and corresponding eigenvectors
sorted_indices = torch.argsort(eigenvalues.real, descending=True)
eigenvalues = eigenvalues[sorted_indices]
eigenvectors = eigenvectors[:, sorted_indices].to(centered_data.dtype)
# Pick the first two components
principal_components = eigenvectors[:, :2]*eigenvalues[:2].real
# Plot the original data with eigenvectors
plt.scatter(tensor_data[:, 0], tensor_data[:, 1], c=labels, cmap='viridis', label='Original Data')
plt.axis('equal')
plt.arrow(mean[0], mean[1], principal_components[0, 0], principal_components[1, 0], color='red', label='PC1')
plt.arrow(mean[0], mean[1], principal_components[0, 1], principal_components[1, 1], color='blue', label='PC2')
# Plot an ellipse around the Eigenvectors
angle = torch.atan2(principal_components[1,1],principal_components[0,1]).detach().numpy()/3.1415*180
ellipse=pat.Ellipse((mean[0].detach(), mean[1].detach()), 2*torch.norm(principal_components[:,1]), 2*torch.norm(principal_components[:,0]), angle=angle, fill=False)
ax = plt.gca()
ax.add_patch(ellipse)
plt.legend()
plt.show()
Note that the output of the PCA function is not necessarily sorted by the largest Eigenvalue. We are using the real part of each Eigenvalue for this and plot the resulting Eigenvectors below. Also note that we multiply each Eigenvector with the real part of its Eigenvalue to scale them.
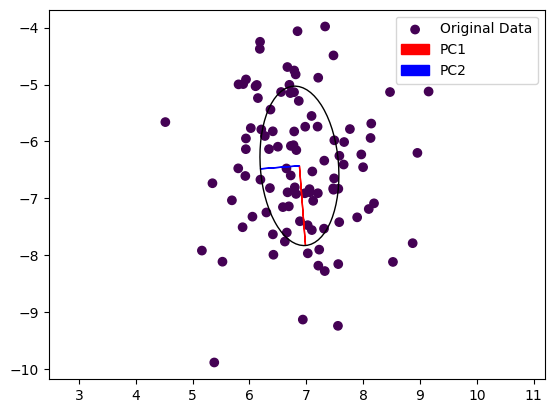
We can see that the first principal component, the dominant Eigenvector, is aligned with the longer axes of our random point cloud, whereas the second Eigenvector is aligned with the shorter axis. In a robotic application, we could now grasp this object by turning our gripper so that it is parallel to PC1 and close it along PC2. This of course works also in 3D, allowing us to also adjust the gripper’s pitch.
But what does the PCA function actually do? In practice, PCA is implemented using a singular value decomposition as solving the deterministic equation det(A−λI)=0 to find the Eigenvalues λ of a matrix A and hence computing the Eigenvectors might be infeasible. We will instead look at a simple numerical method to build some intution.
The power iteration method is a simple and intuitive algorithm used to find the dominant eigenvector and eigenvalue of a square matrix. It’s particularly useful in the context of data science and machine learning when dealing with large, high-dimensional datasets, if only the first few Eigenvectors are needed.
An eigenvector is a non-zero vector that, when multiplied by a square matrix, results in a scaled version of the same vector. In other words, if A is a square matrix and v is a non-zero vector, then v is an eigenvector of A if there exists a scalar λ (called the eigenvalue) such that:
Av=λv
Here:
In other words, the matrix is reduced to a single number when multiplying its Eigenvectors. The power iteration method takes advantage of this by simply multiplying a random vector with A over and over again, and normalizing it.
Here’s a breakdown of the power iteration method:
And here is the code:
def power_iteration(A, num_iterations=100):
# 1. Initialize a random vector
v = torch.randn(A.shape[1], 1, dtype=A.dtype)
for _ in range(num_iterations):
# 2. Multiply matrix by current vector and normalize
v = torch.matmul(A, v)
v /= torch.norm(v)
# 3. Repeat
# Compute the dominant eigenvalue
eigenvalue = torch.matmul(torch.matmul(v.t(), A), v)
return eigenvalue.item(), v.squeeze()
# Example: find the dominant eigenvector and Eigenvalue of a covariance matrix
dominant_eigenvalue, dominant_eigenvector = power_iteration(covariance_matrix)
In essence, the power iteration method leverages the repeated application of the matrix to a vector, causing the vector to align with the dominant eigenvector. It’s a straightforward and computationally efficient method, especially useful for large datasets where direct computation of eigenvectors may be impractical.
Power iteration finds only the dominant eigenvector and eigenvalue. In order to find the next Eigenvector, we need to flatten the matrix. For this, we subtract the contribution of an Eigenvector from the original matrix:
A′=A−λvv^t
or in code:
def deflate_matrix(A, eigenvalue, eigenvector):
deflated_matrix = A - eigenvalue * torch.matmul(eigenvector, eigenvector.t())
return deflated_matrix
The purpose of obtaining a deflated matrix is to facilitate the iterative computation of subsequent eigenvalues and eigenvectors. After finding the first eigenvalue-eigenvector pair, you can use the deflated matrix to find the next one, and so on.
The result of this approach is not necessarily orthogonal, however. Gram-Schmidt orthogonalization is a process in linear algebra used to transform a set of linearly independent vectors into a set of orthogonal (perpendicular) vectors. This method is named after mathematicians Jørgen Gram and Erhard Schmidt and is particularly useful when working with non-orthogonal bases.
def gram_schmidt(v, u):
# Gram-Schmidt orthogonalization
projection = torch.matmul(u.t(), v) / torch.matmul(u.t(), u)
v = v.squeeze(-1) - projection * u
return v
We can now add Gram-Schmidt Orthogonalization to the Power Method and compute both the Dominant and the Second Eigenvector:
# Power iteration to find dominant eigenvector
dominant_eigenvalue, dominant_eigenvector = power_iteration(covariance_matrix)
deflated_matrix = deflate_matrix(covariance_matrix, dominant_eigenvalue, dominant_eigenvector)
second_eigenvector = deflated_matrix[:, 0].view(-1, 1)
# Power iteration to find the second eigenvector
for _ in range(100):
second_eigenvector = torch.matmul(covariance_matrix, second_eigenvector)
second_eigenvector /= torch.norm(second_eigenvector)
# Orthogonalize with respect to the first eigenvector
second_eigenvector = gram_schmidt(second_eigenvector, dominant_eigenvector)
second_eigenvalue = torch.matmul(torch.matmul(second_eigenvector.t(), covariance_matrix), second_eigenvector)
We can now plot the Eigenvectors computed with either method next to each other:
# Scale Eigenvectors by Eigenvalues
dominant_eigenvector *= dominant_eigenvalue
second_eigenvector *= second_eigenvalue
# Plot the original data with eigenvectors computed either way
plt.scatter(tensor_data[:, 0], tensor_data[:, 1], c=labels, cmap='viridis', label='Original Data')
plt.axis('equal')
plt.arrow(mean[0], mean[1], principal_components[0, 0], principal_components[1, 0], color='red', label='PC1')
plt.arrow(mean[0], mean[1], principal_components[0, 1], principal_components[1, 1], color='blue', label='PC2')
plt.arrow(mean[0], mean[1], dominant_eigenvector[0], dominant_eigenvector[1], color='orange', label='approx1')
plt.arrow(mean[0], mean[1], second_eigenvector[0], second_eigenvector[1], color='purple', label='approx2')
plt.legend()
plt.show()
…and the result is:
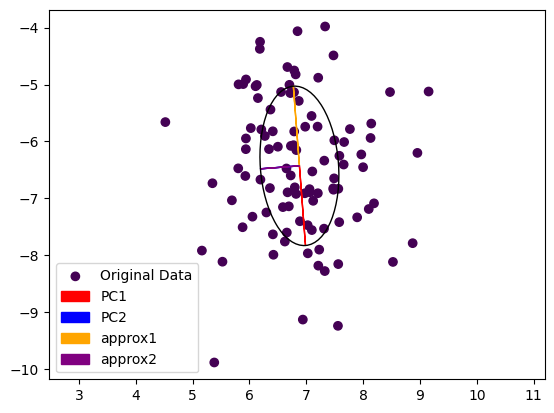
Note that the second Eigenvector coming from power iteration (purple) is painted over the second Eigenvector computed by the exact method (blue). The dominant Eigenvector from power iteration (yellow) is pointing in the other direction then the exact dominant Eigenvector (red). This is not really surprising, as we started from a random vector during power iteration and the result could come out either way.
We presented a simple numerical method to compute the Eigenvectors of a Covariance Matrix to derive the Principal Components of a dataset, shedding some light on the properties of Eigenvectors and Eigenvalues.
Understanding Principal Component Analysis in PyTorch was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Originally appeared here:
Understanding Principal Component Analysis in PyTorch
Go Here to Read this Fast! Understanding Principal Component Analysis in PyTorch